mcfx's blog

题解、Writeup、游记和碎碎念

0CTF/TCTF 2020 Quals Writeup

目录

Crypto

babyring

我们需要给出 64 个数，cur 每次会异或上一个数，然后用 RC4 加密一次，最后得到原来的 cur。RC4 本质上也是在异或，所以就是说，给出的 64 个数，其异或和需要与指定值相等。

虽然这个指定值是和密钥有关的，是可控的，但是他也是近似随机的，所以可以随便钦定一个密钥。

给出的 64 个数，每个数是 yi=xie mod Niy_i=x_i^e\bmod N_i，其中 xix_i 可控，NiN_i 难以被分解，所以也可以近似当成随机的。

既然这些数全是随机的，那么可以考虑 Meet in Middle 算法。比如可以让前 62 个 yiy_i 都是 00，最后两个 yiy_i 各随机 O(232)O(2^{32}) 个，期望就有较高概率找到满足条件的值。

但是这里的时间瓶颈是计算 xe mod Nix^e\bmod N_i，所以可以把最后 6 个 yiy_i 都随机 10000 个，然后把前三个和后三个拿来匹配。

这个是随机 yiy_i 的脚本：

from Crypto.Cipher import ARC4
from hashlib import sha256
from data import K,e,Ns
from struct import pack, unpack

msg=b'123'
key = sha256(msg).digest()[:16]
E = ARC4.new(key)
RC4_all=ARC4.new(key).encrypt(b'\0'*8*64)
rk=0
for i in range(64):
    t=i
    rk^=unpack('Q',RC4_all[t*8:t*8+8])[0]
print(rk)
for i in range(6):
    s=''
    for j in range(10000):
        s+=str(pow(j,e,Ns[K-6+i])%(1<<64))+' '
    print(s)

这个是 Meet in Middle 的：

#include<bits/stdc++.h>

typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef double lf;
typedef long double llf;
typedef std::pair<int,int> pii;

#define xx first
#define yy second

template<typename T> inline T max(T a,T b){return a>b?a:b;}
template<typename T> inline T min(T a,T b){return a<b?a:b;}
template<typename T> inline T abs(T a){return a>0?a:-a;}
template<typename T> inline bool repr(T &a,T b){return a<b?a=b,1:0;}
template<typename T> inline bool repl(T &a,T b){return a>b?a=b,1:0;}
template<typename T> inline T gcd(T a,T b){T t;if(a<b){while(a){t=a;a=b%a;b=t;}return b;}else{while(b){t=b;b=a%b;a=t;}return a;}}
template<typename T> inline T sqr(T x){return x*x;}
#define mp(a,b) std::make_pair(a,b)
#define pb push_back
#define I __attribute__((always_inline))inline
#define mset(a,b) memset(a,b,sizeof(a))
#define mcpy(a,b) memcpy(a,b,sizeof(a))

#define fo0(i,n) for(int i=0,i##end=n;i<i##end;i++)
#define fo1(i,n) for(int i=1,i##end=n;i<=i##end;i++)
#define fo(i,a,b) for(int i=a,i##end=b;i<=i##end;i++)
#define fd0(i,n) for(int i=(n)-1;~i;i--)
#define fd1(i,n) for(int i=n;i;i--)
#define fd(i,a,b) for(int i=a,i##end=b;i>=i##end;i--)
#define foe(i,x)for(__typeof((x).end())i=(x).begin();i!=(x).end();++i)
#define fre(i,x)for(__typeof((x).rend())i=(x).rbegin();i!=(x).rend();++i)

struct Cg{I char operator()(){return getchar();}};
struct Cp{I void operator()(char x){putchar(x);}};
#define OP operator
#define RT return *this;
#define UC unsigned char
#define RX x=0;UC t=P();while((t<'0'||t>'9')&&t!='-')t=P();bool f=0;\
if(t=='-')t=P(),f=1;x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define RL if(t=='.'){lf u=0.1;for(t=P();t>='0'&&t<='9';t=P(),u*=0.1)x+=u*(t-'0');}if(f)x=-x
#define RU x=0;UC t=P();while(t<'0'||t>'9')t=P();x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define TR *this,x;return x;
I bool IS(char x){return x==10||x==13||x==' ';}template<typename T>struct Fr{T P;I Fr&OP,(int&x)
{RX;if(f)x=-x;RT}I OP int(){int x;TR}I Fr&OP,(ll &x){RX;if(f)x=-x;RT}I OP ll(){ll x;TR}I Fr&OP,(char&x)
{for(x=P();IS(x);x=P());RT}I OP char(){char x;TR}I Fr&OP,(char*x){char t=P();for(;IS(t);t=P());if(~t){for(;!IS
(t)&&~t;t=P())*x++=t;}*x++=0;RT}I Fr&OP,(lf&x){RX;RL;RT}I OP lf(){lf x;TR}I Fr&OP,(llf&x){RX;RL;RT}I OP llf()
{llf x;TR}I Fr&OP,(uint&x){RU;RT}I OP uint(){uint x;TR}I Fr&OP,(ull&x){RU;RT}I OP ull(){ull x;TR}};Fr<Cg>in;
#define WI(S) if(x){if(x<0)P('-'),x=-x;UC s[S],c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
#define WL if(y){lf t=0.5;for(int i=y;i--;)t*=0.1;if(x>=0)x+=t;else x-=t,P('-');*this,(ll)(abs(x));P('.');if(x<0)\
x=-x;while(y--){x*=10;x-=floor(x*0.1)*10;P(((int)x)%10+'0');}}else if(x>=0)*this,(ll)(x+0.5);else *this,(ll)(x-0.5);
#define WU(S) if(x){UC s[S],c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
template<typename T>struct Fw{T P;I Fw&OP,(int x){WI(10);RT}I Fw&OP()(int x){WI(10);RT}I Fw&OP,(uint x){WU(10);RT}
I Fw&OP()(uint x){WU(10);RT}I Fw&OP,(ll x){WI(19);RT}I Fw&OP()(ll x){WI(19);RT}I Fw&OP,(ull x){WU(20);RT}I Fw&OP()
(ull x){WU(20);RT}I Fw&OP,(char x){P(x);RT}I Fw&OP()(char x){P(x);RT}I Fw&OP,(const char*x){while(*x)P(*x++);RT}
I Fw&OP()(const char*x){while(*x)P(*x++);RT}I Fw&OP()(lf x,int y){WL;RT}I Fw&OP()(llf x,int y){WL;RT}};Fw<Cp>out;

using namespace std;

const uint N=10000,N2=N*N;
const ull C=6442450944ull;

ull rk,s[6][N];

int main()
{
    freopen("in.txt","r",stdin);
    in,rk;
    fo0(i,6)fo0(j,N)in,s[i][j];
    std::vector<ull>v1;
    v1.reserve(C);
    for(ull t=0;t<C;t++)
    {
        if(t%0x400000==0)out,t,' ',v1.size(),'\n';
        v1.pb(s[0][t/N2]^s[1][t/N%N]^s[2][t%N]^rk);
    }
    out,"sorting...\n";
    std::sort(v1.begin(),v1.end());
    out,"checking...\n";
#pragma omp parallel for
    for(ull i=0;i<(ull)N*N*N;i++)
    {
        ull t=s[3][i/N2]^s[4][i/N%N]^s[5][i%N];
        ull*s=std::lower_bound(v1.data(),v1.data()+C,t);
        if(s!=v1.data()+C&&*s==t)
        {
            out,i,' ',t,'\n';
        }
    }
}

上面输出 ii 和 tt 之后，还需要进一步找出 tt 的来源（改一下第一个 for 即可）。

最后把 tt 的来源和 ii 填入下面的 k1,k2k1,k2 即可：

from pwn import *
from Crypto.Cipher import ARC4
from hashlib import sha256
from data import K,e,Ns
from struct import pack, unpack
import string

context.log_level='debug'

def PoW():
    r.recvuntil('sha256(XXXX+')
    s=r.recv(16)
    r.recvuntil(') == ')
    hs=r.recv(64).decode()
    ch=string.ascii_letters+string.digits
    for i in ch:
        for j in ch:
            for k in ch:
                for l in ch:
                    t=(i+j+k+l).encode()+s
                    if sha256(t).hexdigest()==hs:
                        r.send(i+j+k+l+'\n')
                        return

r=remote('pwnable.org',10001)
PoW()

r.recvuntil('message: ')
msg = b'123'
r.send(msg+b'\n')

k1=6426092827
k2=750365124963
N=10000
N2=N*N
x=[0]*(K-6)+[k1//N2,k1//N%N,k1%N,k2//N2,k2//N%N,k2%N]

for i in range(K):
    r.recvuntil('x%d: '%i)
    r.send(str(x[i])+'\n')
r.send('0\n')
r.interactive()

emmm

题目给出了一个块加密，加密函数如下：

def encrypt_block(x):
    tmp = x * K0 % P
    tmp = tmp * C % M
    tmp = tmp * K1 % P
    return tmp

其中 PP 是个 2582^{58} 量级的质数，CC 是另一个质数，M=260M=2^{60}，K0,K1K_0,K_1 是随机的。同时还给出了 2242^{24} 个随机明密文对。

假设 aa 对应的密文是 bb，即

b=((a⋅K0 mod P)⋅C mod M)⋅K1 mod Pb=((a\cdot K_0\bmod P)\cdot C\bmod M)\cdot K_1\bmod P

那么

b⋅K1−1≡(a⋅K0 mod P)⋅C mod M(modP)b\cdot K_1^{-1}\equiv (a\cdot K_0\bmod P)\cdot C\bmod M\pmod P

考虑找一些 bb（假设找到了 nn 组 a,ba,b：a1,…,ana_1,\dots,a_n 和 b1,…bnb_1,\dots b_n），使得他们的和是 PP 的倍数，那么存在 kk 使得

kP=∑i=1n(ai⋅K0 mod P)⋅C mod MkP=\sum\limits_{i=1}^n (a_i\cdot K_0\bmod P)\cdot C\bmod M

这里假设 nn 很小（后面再讲怎么找这些 bb），那么 kk 也很小，枚举 kk，可以得到

kP mod M=(∑i=1nai⋅K0 mod P)⋅C mod MkP\bmod M=\left(\sum\limits_{i=1}^n a_i\cdot K_0\bmod P\right)\cdot C\bmod M

把 CC 移到左边，令 k⋅P⋅C−1 mod M=tk\cdot P\cdot C^{-1}\bmod M=t，那么

t=(∑i=1nai⋅K0 mod P) mod Mt=\left(\sum\limits_{i=1}^n a_i\cdot K_0\bmod P\right)\bmod M

即存在 qq 使得

t+qM=∑i=1nai⋅K0 mod Pt+qM=\sum\limits_{i=1}^n a_i\cdot K_0\bmod P

同样，这里 qq 也很小，可以枚举，最后可以得到

(t+qM) mod P=(∑i=1nai)⋅K0 mod P(t+qM)\bmod P=\left(\sum\limits_{i=1}^n a_i\right)\cdot K_0\bmod P

这样就可以直接计算出 K0K_0 了。之后算 flag 自然也是水到渠成的。

不过还有个小问题，怎么找出这些和为 PP 的倍数的 bb。考虑把前 60 个 bb 拿出来，如果把所有 2602^{60} 个子集和算出来，那么有较高概率在其中发现一个特定的数。PP 的倍数有很多，所以这个做法期望是能找出的（即使前 60 个不行，也可以多随机几次）。实际上也不需要找出所有 2602^{60} 个子集和。可以类似 Meet in Middle 的做法，枚举出前 3030 个 bb 的 2302^{30} 个子集和（后 3030 个 bb 也一样），然后双指针扫一遍。

找 bb 的代码：

#include<bits/stdc++.h>

typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef double lf;
typedef long double llf;
typedef std::pair<int,int> pii;

#define xx first
#define yy second

template<typename T> inline T max(T a,T b){return a>b?a:b;}
template<typename T> inline T min(T a,T b){return a<b?a:b;}
template<typename T> inline T abs(T a){return a>0?a:-a;}
template<typename T> inline bool repr(T &a,T b){return a<b?a=b,1:0;}
template<typename T> inline bool repl(T &a,T b){return a>b?a=b,1:0;}
template<typename T> inline T gcd(T a,T b){T t;if(a<b){while(a){t=a;a=b%a;b=t;}return b;}else{while(b){t=b;b=a%b;a=t;}return a;}}
template<typename T> inline T sqr(T x){return x*x;}
#define mp(a,b) std::make_pair(a,b)
#define pb push_back
#define I __attribute__((always_inline))inline
#define mset(a,b) memset(a,b,sizeof(a))
#define mcpy(a,b) memcpy(a,b,sizeof(a))

#define fo0(i,n) for(int i=0,i##end=n;i<i##end;i++)
#define fo1(i,n) for(int i=1,i##end=n;i<=i##end;i++)
#define fo(i,a,b) for(int i=a,i##end=b;i<=i##end;i++)
#define fd0(i,n) for(int i=(n)-1;~i;i--)
#define fd1(i,n) for(int i=n;i;i--)
#define fd(i,a,b) for(int i=a,i##end=b;i>=i##end;i--)
#define foe(i,x)for(__typeof((x).end())i=(x).begin();i!=(x).end();++i)
#define fre(i,x)for(__typeof((x).rend())i=(x).rbegin();i!=(x).rend();++i)

struct Cg{I char operator()(){return getchar();}};
struct Cp{I void operator()(char x){putchar(x);}};
#define OP operator
#define RT return *this;
#define UC unsigned char
#define RX x=0;UC t=P();while((t<'0'||t>'9')&&t!='-')t=P();bool f=0;\
if(t=='-')t=P(),f=1;x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define RL if(t=='.'){lf u=0.1;for(t=P();t>='0'&&t<='9';t=P(),u*=0.1)x+=u*(t-'0');}if(f)x=-x
#define RU x=0;UC t=P();while(t<'0'||t>'9')t=P();x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define TR *this,x;return x;
I bool IS(char x){return x==10||x==13||x==' ';}template<typename T>struct Fr{T P;I Fr&OP,(int&x)
{RX;if(f)x=-x;RT}I OP int(){int x;TR}I Fr&OP,(ll &x){RX;if(f)x=-x;RT}I OP ll(){ll x;TR}I Fr&OP,(char&x)
{for(x=P();IS(x);x=P());RT}I OP char(){char x;TR}I Fr&OP,(char*x){char t=P();for(;IS(t);t=P());if(~t){for(;!IS
(t)&&~t;t=P())*x++=t;}*x++=0;RT}I Fr&OP,(lf&x){RX;RL;RT}I OP lf(){lf x;TR}I Fr&OP,(llf&x){RX;RL;RT}I OP llf()
{llf x;TR}I Fr&OP,(uint&x){RU;RT}I OP uint(){uint x;TR}I Fr&OP,(ull&x){RU;RT}I OP ull(){ull x;TR}};Fr<Cg>in;
#define WI(S) if(x){if(x<0)P('-'),x=-x;UC s[S],c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
#define WL if(y){lf t=0.5;for(int i=y;i--;)t*=0.1;if(x>=0)x+=t;else x-=t,P('-');*this,(ll)(abs(x));P('.');if(x<0)\
x=-x;while(y--){x*=10;x-=floor(x*0.1)*10;P(((int)x)%10+'0');}}else if(x>=0)*this,(ll)(x+0.5);else *this,(ll)(x-0.5);
#define WU(S) if(x){UC s[S],c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
template<typename T>struct Fw{T P;I Fw&OP,(int x){WI(10);RT}I Fw&OP()(int x){WI(10);RT}I Fw&OP,(uint x){WU(10);RT}
I Fw&OP()(uint x){WU(10);RT}I Fw&OP,(ll x){WI(19);RT}I Fw&OP()(ll x){WI(19);RT}I Fw&OP,(ull x){WU(20);RT}I Fw&OP()
(ull x){WU(20);RT}I Fw&OP,(char x){P(x);RT}I Fw&OP()(char x){P(x);RT}I Fw&OP,(const char*x){while(*x)P(*x++);RT}
I Fw&OP()(const char*x){while(*x)P(*x++);RT}I Fw&OP()(lf x,int y){WL;RT}I Fw&OP()(llf x,int y){WL;RT}};Fw<Cp>out;

using namespace std;

const int N=60;
const ull P=247359019496198933;

ull a[N],b[N];

std::vector<ull>get_pack(int st)
{
    std::vector<ull>a,b;
    a.pb(0);
    fo0(i,N/2)
    {
        out,"add item: ",i,'\n';
        b.swap(a);
        a.clear();
        int k=0;
        ull cur=::b[st+i];
        fo0(j,b.size())
        {
            for(;k<b.size()&&b[k]<b[j]+cur;k++)
                a.pb(b[k]);
            a.pb(b[j]+cur);
        }
    }
    return a;
}

int get_sol(int st,ull req)
{
    std::vector<ull>f;
    f.resize(1<<(N/2));
    fo1(i,(1<<(N/2))-1)
    {
        f[i]=f[i&i-1]+b[st+__builtin_ctz(i)];
        if(f[i]==req)return i;
    }
    return -1;
}

int main()
{
    freopen("res","r",stdin);
    fo0(i,N)in,a[i],b[i];
    fo0(i,N)assert(a[i]<P&&b[i]<P);
    std::vector<ull>sa=get_pack(0);
    std::vector<ull>sb=get_pack(N/2);
    fo1(u,74)
    {
        out,"test: ",u,"*P\n";
        ll req=u*P;
        int j=sb.size()-1;
        fo0(i,sa.size())
        {
            if(sa[i]>req)break;
            while(j>=0&&sb[j]>req-sa[i])j--;
            if(j<0)break;
            if(sb[j]==req-sa[i])
            {
                out,"ok:",get_sol(0,sa[i]),' ',get_sol(N/2,sb[j]),'\n';
            }
        }
    }
}

把输出填到下面的 mask 处：

from binascii import unhexlify
import string
printset = set(string.printable.encode())
isprintable = lambda x:set(x).issubset(printset)

P = 247359019496198933
C = 223805275076627807
M = 2**60

def encrypt(x,K0,K1):
    tmp = x * K0 % P
    tmp = tmp * C % M
    tmp = tmp * K1 % P
    return tmp

Cr = 1131579515458719391 # gmpy2.invert(C,M)
assert C*Cr%M==1

mask=792490199|92872563<<30
f=open('res')
s=[]
for i in range(60):
    v=list(map(int,f.readline().strip().split()))
    if mask>>i&1:
        s.append(v)


sum=0
for i in s:
    sum+=i[1]
assert(sum%P==0)
sa=0
for i in s:
    sa+=i[0]
sa_inv=pow(sa,P-2,P)

n=len(s)

for k in range(n*M//P+1):
    for v in range(n*P//M+1):
        ao=(k*P*Cr%M+M*v)%P
        K0=ao*sa_inv%P
        a,b=s[0]
        K1=pow(a*K0%P*C%M,P-2,P)*b%P
        if K0==0 or K1==0:
            continue
        assert (a*K0%P*C%M)*K1%P==b
        assert encrypt(a,K0,K1)==b
        flag=True
        for i in s:
            if encrypt(i[0],K0,K1)!=i[1]:
                flag=False
                break
        if flag:
            K=(K0,K1)
            print(K0,K1)

K0,K1=K
while True:
    flag=f.readline().strip()
    if len(flag)>50:
        break
flag=unhexlify(flag)
fr=b''
for i in range(0,len(flag),8):
    x=int.from_bytes(flag[i:i+8],'little')
    tmp=x*pow(K1,P-2,P)%P
    for j in range(M//P+1):
        tmp2=(tmp+j*P)*Cr%M
        if tmp2<P:
            tmp2=tmp2*pow(K0,P-2,P)%P
            for k in range(2**64//P+1):
                if tmp2+k*P<2**64:
                    res=(tmp2+k*P).to_bytes(8,'little')
                    if isprintable(res):
                        fr+=res
print(fr)

Simple Curve

代码中给出的 C 是一个 Hyperelliptic curve，其运算规则可以在 https://www.math.uwaterloo.ca/~ajmeneze/publications/hyperelliptic.pdf 找到。这篇论文中，30 页附近提到了一些加密相关的东西，比如 order of the jacobian 的计算。算出这个之后，就可以和一般椭圆曲线类似的求出 dd。

按论文中的方法，手动计算出 M1=M2=3M_1=M_2=3，然后用下面的脚本计算 order of the jacobian：

from sympy import *

def work(M1,M2):
    x=symbols('x')
    q=2

    a1=M1-1-q
    a2=x/x*(M2-1-q**2+a1**2)/2

    g1,g2=solve(x**2+a1*x+(a2-2*q))
    a=solve(x**2-g1*x+q)
    b=solve(x**2-g2*x+q)
    return a[0],b[0]

x,y=work(3,3)
n=256
o=simplify(simplify(abs(1-x**n))**2*simplify(abs(1-y**n))**2)
print(o)

然后在原题目环境中计算：

x=F.fetch_int(113832590633816699072296178013238414056344242047498922038140127850188287361982)+w*F.fetch_int(107565990181246983920093578624450838959059911990845389169965709337104431186583)+w*w
y=F.fetch_int(60811562094598445636243277376189331059312500825950206260715002194681628361141)+w*F.fetch_int(109257511993433204574833526052641479730322989843001720806658798963521316354418)

n=13407807929942597099574024998205846127384782207827457971403006387925941306569427075743805985793764139096494648696821820448189053384542053304334065342873600
d=gmpy2.invert(65537,n)
print decode(mul((x,y),d))

得到

([87336973591408809511144500944284390061575902317760214640835643492103517747L, 1], [13135483297081885116852406153608965390497862234689399731252856847524895364760L])

最后

(87336973591408809511144500944284390061575902317760214640835643492103517747).to_bytes(100,'big')

即可得到 flag。

gene

文件中静态链接了 OpenSSL，对于这部分函数，可以看到有一些类似 (3LL, 148LL, 65LL, "../crypto/bn/bn_ctx.c", 265LL) 的函数调用。猜测是报错，265 是行号，与源文件大致对应可以得到具体是什么函数。

大致还原 OpenSSL 的函数之后，接下来看到，main 中有几个全局的 BIGNUM（暂且记作 gnum1、gnum2、gnum3），同时 gnum2 和 3 是随机的。另外 main 还调用了一个奇怪的函数，太大导致 ida 无法正常反编译。

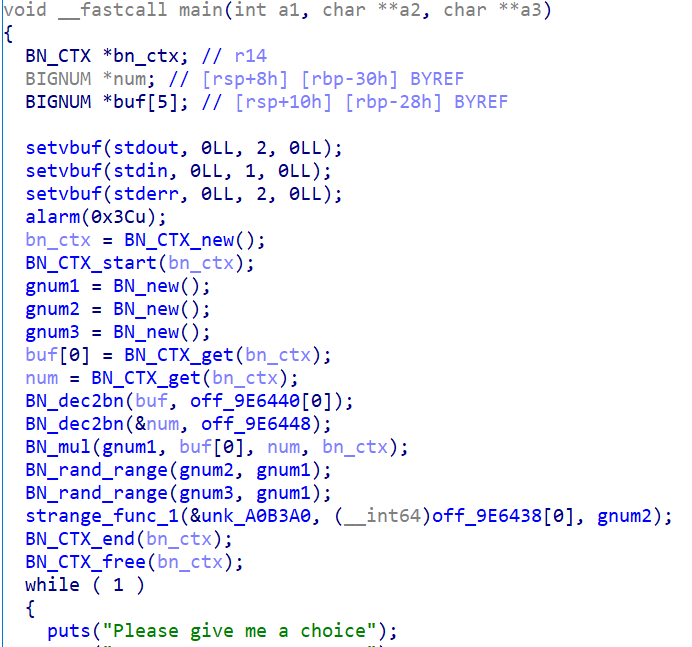
接下来看 sign 部分，可以发现，签名的第一部分是由奇怪的函数对 m0+gnum3m_0+gnum_3 操作得到的，而第二部分是 (sha256(m0+m1)∗gnum2+m0+gnum3) mod gnum1(\text{sha256}(m_0+m_1)*gnum_2+m_0+gnum_3)\bmod gnum_1。

那么 gnum2gnum_2 和 gnum3gnum_3 只需要两组数据，就能解方程解出。这样就可以构造第二部分的签名。而第一部分可以调用程序自身来解，传入 m0+remote gnum3−local gnum3m_0+\text{remote }gnum_3-\text{local }gnum_3 即可。

from pwn import *
from hashlib import sha256
from gmpy2 import invert

gnum1=0xb8a8d9bbe123f017b80b0047445d4184c2c230fcd9cb14874eb4b6a1cf1135dfd2de8ea3604
N=gnum1

def get_eq(r,m0,m1):
    r.recvuntil('4. exit')
    r.recvuntil('> ')
    r.send('1\n')
    r.recvuntil('> ')
    r.send(m0+'\n')
    r.recvuntil('> ')
    r.send(str(len(m1)+3)+'\n')
    r.recvuntil('> ')
    r.send(m1+'\n')
    hs=int(sha256((m0+m1+'\n').encode()).hexdigest(),16)
    m0=int(m0,16)
    r.recvuntil('sig')
    r.recvuntil(', ')
    sig=int(r.recvuntil(')')[:-1],16)
    return hs,(sig-m0)%gnum1

def get_gnum(r):
    m0='114514'
    i=0
    while True:
        a1,b1=get_eq(r,m0,str(i))
        a2,b2=get_eq(r,m0,str(i+1))
        i+=2
        try:
            gnum2=(b1-b2)%N*invert((a1-a2)%N,N)%N
            gnum3=(b1-a1*gnum2)%N
            assert gnum3==(b2-a2*gnum2)%N
            break
        except:
            pass
    return gnum2,gnum3

r=remote('pwnable.org',23334)
r2,r3=get_gnum(r)
print(r2,r3)
r.recvuntil('4. exit')
r.recvuntil('> ')
r.send('3\n')
r.recvuntil('m0 = ')
req_m0o=r.recvuntil(' ')[:-1]
req_m0=int(req_m0o,16)
print('req:',req_m0o)

while True:
    lo=process('./gene')
    l2,l3=get_gnum(lo)
    if req_m0>l3:
        break
    lo.close()
    print('local retry')
print(l2,l3)

v=hex(req_m0+r3-l3)[2:].upper()
lo.recvuntil('4. exit')
lo.recvuntil('> ')
lo.send('1\n')
lo.recvuntil('> ')
lo.send(v+'\n')
lo.recvuntil('> ')
lo.send('12\n')
lo.recvuntil('> ')
lo.send('show_me_flag')
lo.recvuntil('The sig')
lo.recvuntil('(')
sig1=lo.recvuntil(', ')[:-2]
lo.close()
print('sig1:',sig1)

hs=int(sha256(req_m0o+b'show_me_flag').hexdigest(),16)
sig2=(hs*r2+req_m0+r3)%N
sig2=hex(sig2)[2:].upper()
if len(sig2)%2:
    sig2='0'+sig2
print('sig2:',sig2)

r.recvuntil('> ')
r.send(sig1)
r.recvuntil('> ')
r.send(sig2)
r.interactive()

Reverse

babymips

在 https://codescape.mips.com/components/toolchain/nanomips/2019.03-06/downloads.html 下载各种库，然后 objdump 导出汇编。

balc 是调用函数，据此可以分离出各个函数。主函数在 4006e4。

程序首先读入 flag，检查前 5 位是否是 flag{，然后把接下来的部分依次填入 420000 开始的空位中。接下来调用 4006b6 检查 flag，而 4006b6 又调用了 400580、4005ee、400652 三个函数。这三个函数都是在进行一些操作之后调用 4004c6。

这三个函数的操作是，每次从 420000 拷贝 9 字节到栈上，然后 4004c6 会检查这 9 字节中是否 acdeqswxz 各出现恰好一次。400580 根据一个表来拷贝，如果把 420000 开始的部分当成 9*9 方阵，那么 4005ee 和 400652 分别根据行和列拷贝。

这个规则类似数独，写一个暴搜就能搜出 flag。

#include<bits/stdc++.h>

typedef unsigned int uint;
typedef long long ll;
typedef unsigned long long ull;
typedef double lf;
typedef long double llf;
typedef std::pair<int,int> pii;

#define xx first
#define yy second

template<typename T> inline T max(T a,T b){return a>b?a:b;}
template<typename T> inline T min(T a,T b){return a<b?a:b;}
template<typename T> inline T abs(T a){return a>0?a:-a;}
template<typename T> inline bool repr(T &a,T b){return a<b?a=b,1:0;}
template<typename T> inline bool repl(T &a,T b){return a>b?a=b,1:0;}
template<typename T> inline T gcd(T a,T b){T t;if(a<b){while(a){t=a;a=b%a;b=t;}return b;}else{while(b){t=b;b=a%b;a=t;}return a;}}
template<typename T> inline T sqr(T x){return x*x;}
#define mp(a,b) std::make_pair(a,b)
#define pb push_back
#define I __attribute__((always_inline))inline
#define mset(a,b) memset(a,b,sizeof(a))
#define mcpy(a,b) memcpy(a,b,sizeof(a))

#define fo0(i,n) for(int i=0,i##end=n;i<i##end;i++)
#define fo1(i,n) for(int i=1,i##end=n;i<=i##end;i++)
#define fo(i,a,b) for(int i=a,i##end=b;i<=i##end;i++)
#define fd0(i,n) for(int i=(n)-1;~i;i--)
#define fd1(i,n) for(int i=n;i;i--)
#define fd(i,a,b) for(int i=a,i##end=b;i>=i##end;i--)
#define foe(i,x)for(__typeof((x).end())i=(x).begin();i!=(x).end();++i)
#define fre(i,x)for(__typeof((x).rend())i=(x).rbegin();i!=(x).rend();++i)

struct Cg{I char operator()(){return getchar();}};
struct Cp{I void operator()(char x){putchar(x);}};
#define OP operator
#define RT return *this;
#define UC unsigned char
#define RX x=0;UC t=P();while((t<'0'||t>'9')&&t!='-')t=P();bool f=0;\
if(t=='-')t=P(),f=1;x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define RL if(t=='.'){lf u=0.1;for(t=P();t>='0'&&t<='9';t=P(),u*=0.1)x+=u*(t-'0');}if(f)x=-x
#define RU x=0;UC t=P();while(t<'0'||t>'9')t=P();x=t-'0';for(t=P();t>='0'&&t<='9';t=P())x=x*10+t-'0'
#define TR *this,x;return x;
I bool IS(char x){return x==10||x==13||x==' ';}template<typename T>struct Fr{T P;I Fr&OP,(int&x)
{RX;if(f)x=-x;RT}I OP int(){int x;TR}I Fr&OP,(ll &x){RX;if(f)x=-x;RT}I OP ll(){ll x;TR}I Fr&OP,(char&x)
{for(x=P();IS(x);x=P());RT}I OP char(){char x;TR}I Fr&OP,(char*x){char t=P();for(;IS(t);t=P());if(~t){for(;!IS
(t)&&~t;t=P())*x++=t;}*x++=0;RT}I Fr&OP,(lf&x){RX;RL;RT}I OP lf(){lf x;TR}I Fr&OP,(llf&x){RX;RL;RT}I OP llf()
{llf x;TR}I Fr&OP,(uint&x){RU;RT}I OP uint(){uint x;TR}I Fr&OP,(ull&x){RU;RT}I OP ull(){ull x;TR}};Fr<Cg>in;
#define WI(S) if(x){if(x<0)P('-'),x=-x;UC s[S],c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
#define WL if(y){lf t=0.5;for(int i=y;i--;)t*=0.1;if(x>=0)x+=t;else x-=t,P('-');*this,(ll)(abs(x));P('.');if(x<0)\
x=-x;while(y--){x*=10;x-=floor(x*0.1)*10;P(((int)x)%10+'0');}}else if(x>=0)*this,(ll)(x+0.5);else *this,(ll)(x-0.5);
#define WU(S) if(x){UC s[S],c=0;while(x)s[c++]=x%10+'0',x/=10;while(c--)P(s[c]);}else P('0')
template<typename T>struct Fw{T P;I Fw&OP,(int x){WI(10);RT}I Fw&OP()(int x){WI(10);RT}I Fw&OP,(uint x){WU(10);RT}
I Fw&OP()(uint x){WU(10);RT}I Fw&OP,(ll x){WI(19);RT}I Fw&OP()(ll x){WI(19);RT}I Fw&OP,(ull x){WU(20);RT}I Fw&OP()
(ull x){WU(20);RT}I Fw&OP,(char x){P(x);RT}I Fw&OP()(char x){P(x);RT}I Fw&OP,(const char*x){while(*x)P(*x++);RT}
I Fw&OP()(const char*x){while(*x)P(*x++);RT}I Fw&OP()(lf x,int y){WL;RT}I Fw&OP()(llf x,int y){WL;RT}};Fw<Cp>out;

const char cs[]="acdeqswxz";
const char init[]="..w...s.....d..w..d.....a...e.w.q.a.e........a..zd..swq....w..sx.d.....zw......dx";
const int ord[81]={0, 1, 2, 3, 10, 12, 13, 14, 19, 4, 5, 6, 15, 24, 25, 33, 42, 51, 7, 8, 16, 17, 26, 34, 35, 43, 52, 9, 18, 27, 36, 45, 54, 55, 63, 72, 11, 20, 21, 28, 29, 30, 37, 46, 39, 22, 23, 31, 32, 40, 49, 58, 66, 67, 38, 47, 48, 56, 57, 64, 65, 73, 74, 41, 50, 59, 60, 61, 68, 75, 76, 77, 44, 53, 62, 69, 70, 71, 78, 79, 80};

int s[9][9],box[9][9],a[9],b[9],c[9];

void dfs(int x,int y)
{
    if(y==9)return dfs(x+1,0);
    if(x==9)
    {
        fo0(i,81)if(init[i]=='.')out,cs[s[i/9][i%9]];
        return;
    }
    if(~s[x][y])return dfs(x,y+1);
    int bx=box[x][y],ta=a[x],tb=b[y],tc=c[bx];
    int mask=ta&tb&tc;
    for(;mask;mask&=mask-1)
    {
        int u=__builtin_ctz(mask),v=~(1<<u);
        s[x][y]=u;
        a[x]=ta&v;
        b[y]=tb&v;
        c[bx]=tc&v;
        dfs(x,y+1);
        a[x]=ta;
        b[y]=tb;
        c[bx]=tc;
    }
    s[x][y]=-1;
}

int main()
{
    int req=6;
    fo0(i,81)
    {
        s[i/9][i%9]=-1;
        fo0(j,9)if(init[i]==cs[j])
            s[i/9][i%9]=j;
        if(s[i/9][i%9]==-1)assert(init[i]=='.'),req++;
    }
    fo0(i,81)box[ord[i]/9][ord[i]%9]=i/9;
    fo0(i,9)a[i]=b[i]=c[i]=511;
    fo0(i,81)
    {
        int t=s[i/9][i%9];
        if(!~t)continue;
        a[i/9]&=~(1<<t);
        b[i%9]&=~(1<<t);
        c[box[i/9][i%9]]&=~(1<<t);
    }
    dfs(0,0);
}

日期： 2020-07-03

标签： CTF Writeup

这是一篇旧文，原始文章及评论可在 https://oldblog.mcfx.us/archives/287/ 查看。